Choose the incorrect statement:

1.	All SHM's have a fixed time period.
2.	All motions having the same time period are SHM.
3.	In SHM, the total energy is proportional to the square of the amplitude.
4.	Phase constant of SHM depends on initial conditions.

If a simple pendulum is suspended from the roof of a trolley which moves in the horizontal direction with an acceleration a, then the time period is given by $\mathrm{T} = 2\mathrm{\pi }\sqrt{\frac{\mathrm{l}}{\mathrm{g}\text{'}}}$, where $g\text{'}$ is equal to:

1.  g

2.  g - a

3.  g + a 

4.  $\sqrt{{\mathrm{g}}^2 + {\mathrm{a}}^2}$

In the given figure, when two identical springs are attached with a body of mass m, then oscillation frequency is f. If one spring is removed, then the frequency will become

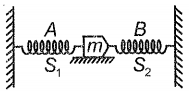
1.  f

2.  2f

3.  $\sqrt{2f}$

4.  $\frac{f}{\sqrt{2}}$

The function ${\sin }^2\left(\omega t\right)$ represents:

1.  An SHM with a period of $\frac{2\mathrm{\pi }}{\mathrm{\omega }}$

2.  An SHM with a period of $\frac{\mathrm{\pi }}{\mathrm{\omega }}$

3.  A periodic motion but not SHM with a period of $\frac{2\mathrm{\pi }}{\mathrm{\omega }}$

4.  A periodic motion but not SHM with a period of $\frac{\mathrm{\pi }}{\mathrm{\omega }}$

Values of the acceleration A of a particle moving in simple harmonic motion as a function of its displacement x are given below

$\mathbf{A}\mathbf{ }\mathbf{\left(}\mathbf{mms}{\mathbf{-}}^{\mathbf{2}}\mathbf{\right)}$      16   8   0   8   -16

x  (mm)                  4    -2   0   2     4

The period of the motion is :

1.  $\frac{1}{\mathrm{\pi }}\mathrm{s}$

2.  $\frac{2}{\mathrm{\pi }}\mathrm{s}$

3.  $\frac{\mathrm{\pi }}{2}s$

4.  $\mathrm{\pi s}$

The acceleration-time graph of a particle undergoing SHM is shown in the figure. Then,

A body of mass M is situated in a potential field. The potential energy of the body is given by $\mathrm{U}\left(\mathrm{x}\right) = {\mathrm{U}}_0\left[1 - \cos \mathrm{Kx}\right]$; where x is position, K and ${\mathrm{U}}_0$ are constant. Period of small oscillations of the body will be:

1.  $2\mathrm{\pi }\sqrt{{\mathrm{MU}}_0{\mathrm{K}}^2}$

2.  $2\mathrm{\pi }\sqrt{\frac{\mathrm{M}}{{\mathrm{U}}_0{\mathrm{K}}^2}}$

3.  $2\mathrm{\pi }\sqrt{\frac{{\mathrm{U}}_0{\mathrm{K}}^2}{\mathrm{M}}}$

4.  $2\mathrm{\pi }\sqrt{\frac{{\mathrm{U}}_0}{{\mathrm{MK}}^2}}$

A particle is executing SHM about origin along X-axis, between points A($\alpha$, 0) and B(-$\alpha$, 0). Its time period of oscillation is T. The magnitude of its acceleration $\frac{\mathrm{T}}{12}$ second after the particle reaches point A will be

1.  $2\sqrt{3}\frac{\mathrm{\pi }}{\mathrm{T}}\mathrm{\alpha }$

2.  $2\sqrt{2}\frac{{\mathrm{\pi }}^2}{{\mathrm{T}}^2}\mathrm{\alpha }$

3.  $2\sqrt{3}\frac{{\mathrm{\pi }}^2}{{\mathrm{T}}^2}\mathrm{\alpha }$

4.  $\sqrt{3}\frac{{\mathrm{\pi }}^2}{{\mathrm{T}}^2}\mathrm{\alpha }$

A particle executes linear oscillation such that its epoch is zero. The ratio of the magnitude of its displacement in 1st second and 2nd second is (Time period = 12 seconds)

1.  $\frac{1}{\sqrt{3} + 1}$

2.  $\frac{1}{\sqrt{3} - 1}$

3.  $\frac{\sqrt{3} - 1}{2}$

4.  $\frac{\sqrt{3}}{\sqrt{3} - 1}$