In the given figure, when two identical springs are attached with a body of mass m, then oscillation frequency is f. If one spring is removed, then the frequency will become

                     

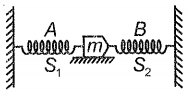
1.  f

2.  2f

3.  $\sqrt{2f}$

4.  $\frac{f}{\sqrt{2}}$

The function ${\sin }^2\left(\omega t\right)$ represents:

1.  An SHM with a period of $\frac{2\mathrm{\pi }}{\mathrm{\omega }}$

2.  An SHM with a period of $\frac{\mathrm{\pi }}{\mathrm{\omega }}$

3.  A periodic motion but not SHM with a period of $\frac{2\mathrm{\pi }}{\mathrm{\omega }}$

4.  A periodic motion but not SHM with a period of $\frac{\mathrm{\pi }}{\mathrm{\omega }}$

Values of the acceleration A of a particle moving in simple harmonic motion as a function of its displacement x are given below

$\mathbf{A}\mathbf{ }\mathbf{\left(}\mathbf{mms}{\mathbf{-}}^{\mathbf{2}}\mathbf{\right)}$      16   8   0   8   -16

x  (mm)                  4    -2   0   2     4

The period of the motion is :

1.  $\frac{1}{\mathrm{\pi }}\mathrm{s}$

2.  $\frac{2}{\mathrm{\pi }}\mathrm{s}$

3.  $\frac{\mathrm{\pi }}{2}s$

4.  $\mathrm{\pi s}$

The acceleration-time graph of a particle undergoing SHM is shown in the figure. Then,

A body of mass M is situated in a potential field. The potential energy of the body is given by $\mathrm{U}\left(\mathrm{x}\right) = {\mathrm{U}}_0\left[1 - \cos \mathrm{Kx}\right]$; where x is position, K and ${\mathrm{U}}_0$ are constant. Period of small oscillations of the body will be:

1.  $2\mathrm{\pi }\sqrt{{\mathrm{MU}}_0{\mathrm{K}}^2}$

2.  $2\mathrm{\pi }\sqrt{\frac{\mathrm{M}}{{\mathrm{U}}_0{\mathrm{K}}^2}}$

3.  $2\mathrm{\pi }\sqrt{\frac{{\mathrm{U}}_0{\mathrm{K}}^2}{\mathrm{M}}}$

4.  $2\mathrm{\pi }\sqrt{\frac{{\mathrm{U}}_0}{{\mathrm{MK}}^2}}$

A particle is executing SHM about origin along X-axis, between points A($\alpha$, 0) and B(-$\alpha$, 0). Its time period of oscillation is T. The magnitude of its acceleration $\frac{\mathrm{T}}{12}$ second after the particle reaches point A will be

1.  $2\sqrt{3}\frac{\mathrm{\pi }}{\mathrm{T}}\mathrm{\alpha }$

2.  $2\sqrt{2}\frac{{\mathrm{\pi }}^2}{{\mathrm{T}}^2}\mathrm{\alpha }$

3.  $2\sqrt{3}\frac{{\mathrm{\pi }}^2}{{\mathrm{T}}^2}\mathrm{\alpha }$

4.  $\sqrt{3}\frac{{\mathrm{\pi }}^2}{{\mathrm{T}}^2}\mathrm{\alpha }$

A particle executes linear oscillation such that its epoch is zero. The ratio of the magnitude of its displacement in 1st second and 2nd second is (Time period = 12 seconds)

1.  $\frac{1}{\sqrt{3} + 1}$

2.  $\frac{1}{\sqrt{3} - 1}$

3.  $\frac{\sqrt{3} - 1}{2}$

4.  $\frac{\sqrt{3}}{\sqrt{3} - 1}$

A block of mass 0.02 kg is connected with spring and is free to oscillate on a horizontal smooth surface as shown. The angular frequency of oscillation is 2 rad ${\mathrm{s}}^{-1}$. The block is pulled by 4 cm (from equilibrium position) and then pushed towards the spring with a velocity of 8 cm/s. The amplitude of oscillation is (Neglect any damping)

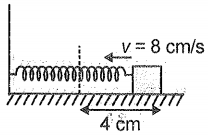
1.  $3\sqrt{2} \mathrm{cm}$

2.  $4\sqrt{2} \mathrm{cm}$

3.  $2\sqrt{2} \mathrm{cm}$

4.  1 cm

A particle moves on a circular path with uniform speed about the origin. The \((x-t)\) graph will be:
(\(x:\) value of \(x-\)coordinate; \(t-\)time)

1.		2.
3.		4.