A particle executes linear oscillation such that its epoch is zero. The ratio of the magnitude of its displacement in 1st second and 2nd second is (Time period = 12 seconds)

1.  $\frac{1}{\sqrt{3} + 1}$

2.  $\frac{1}{\sqrt{3} - 1}$

3.  $\frac{\sqrt{3} - 1}{2}$

4.  $\frac{\sqrt{3}}{\sqrt{3} - 1}$

A block of mass 0.02 kg is connected with spring and is free to oscillate on a horizontal smooth surface as shown. The angular frequency of oscillation is 2 rad ${\mathrm{s}}^{-1}$. The block is pulled by 4 cm (from equilibrium position) and then pushed towards the spring with a velocity of 8 cm/s. The amplitude of oscillation is (Neglect any damping)

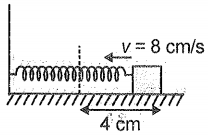
1.  $3\sqrt{2} \mathrm{cm}$

2.  $4\sqrt{2} \mathrm{cm}$

3.  $2\sqrt{2} \mathrm{cm}$

4.  1 cm

A particle moves on a circular path with uniform speed about the origin. The \((x-t)\) graph will be:
(\(x:\) value of \(x-\)coordinate; \(t-\)time)

1.		2.
3.		4.

A simple pendulum has time period \(T.\) The bob is given negative charge and surface below it is given a positive charge. The new time period will be:
1. less than \(T\)
2. greater than \(T\)
3. equal to \(T\)
4. infinite

A simple pendulum attached to the ceiling of a stationary lift has a time period of 1 s. The distance y covered by the lift moving downward varies with time as y = 3.75 ${\mathrm{t}}^2$, where y is in meters and t is in seconds. If g = 10 $\mathrm{m}/{\mathrm{s}}^2$, then the time period of the pendulum will be:

Which of the following may represent the potential energy of a body in S.H.M.? (Symbols have usual meaning)
1. ${\mathrm{m\omega }}^2{\mathrm{A}}^2$
2. $\frac{1}{2}{\mathrm{m\omega }}^2{\mathrm{X}}^2$
3. $\left(2{\mathrm{A}}^2 + \frac{1}{{\mathrm{m\omega }}^2}\right)$
4. both (2) and (3)

A particle moves according $\mathrm{x} = \left(6 \mathrm{cm}\right) \cos \left(\frac{\mathrm{\pi }}{2}\mathrm{t}\right)$. Average velocity of the particle in the time interval between t = 0 to t = 3 s is

1.  1 cm/s

2.  3.5 cm/s

3.  2 cm/s

4.  6 cm/s

A particle performs SHM with frequency \(f.\) The frequency of its velocity and acceleration are respectively:
1. \(f,~f\)
2. \(\frac{f}{2},~f\)
3. \(2f,~f\)
4. \(f,~2f\)

Force acting on a body free to move on the \(\mathrm{X}\)-axis is given by, \(F=-kx^n\) where \(k\) is a positive constant. For which value of \(n\) motion of the body is not oscillatory?

In a forced oscillation, when the system oscillates under the action of the driving force $\mathrm{F}$ $=$ ${\mathrm{F}}_0$ $\sin$ $\mathrm{\omega t}$ in addition to its internal restoring force, the particle oscillates with a frequency equal to

1.  The natural frequency of the body

2.  Frequency of driving force

3.  The difference in frequency of driving force and natural frequency

4.  Mean of the driving frequency and natural frequency