A body of mass M is situated in a potential field. The potential energy of the body is given by $\mathrm{U}\left(\mathrm{x}\right) = {\mathrm{U}}_0\left[1 - \cos \mathrm{Kx}\right]$; where x is position, K and ${\mathrm{U}}_0$ are constant. Period of small oscillations of the body will be:

1.  $2\mathrm{\pi }\sqrt{{\mathrm{MU}}_0{\mathrm{K}}^2}$

2.  $2\mathrm{\pi }\sqrt{\frac{\mathrm{M}}{{\mathrm{U}}_0{\mathrm{K}}^2}}$

3.  $2\mathrm{\pi }\sqrt{\frac{{\mathrm{U}}_0{\mathrm{K}}^2}{\mathrm{M}}}$

4.  $2\mathrm{\pi }\sqrt{\frac{{\mathrm{U}}_0}{{\mathrm{MK}}^2}}$

A particle is executing SHM about origin along X-axis, between points A($\alpha$, 0) and B(-$\alpha$, 0). Its time period of oscillation is T. The magnitude of its acceleration $\frac{\mathrm{T}}{12}$ second after the particle reaches point A will be

1.  $2\sqrt{3}\frac{\mathrm{\pi }}{\mathrm{T}}\mathrm{\alpha }$

2.  $2\sqrt{2}\frac{{\mathrm{\pi }}^2}{{\mathrm{T}}^2}\mathrm{\alpha }$

3.  $2\sqrt{3}\frac{{\mathrm{\pi }}^2}{{\mathrm{T}}^2}\mathrm{\alpha }$

4.  $\sqrt{3}\frac{{\mathrm{\pi }}^2}{{\mathrm{T}}^2}\mathrm{\alpha }$

A particle executes linear oscillation such that its epoch is zero. The ratio of the magnitude of its displacement in 1st second and 2nd second is (Time period = 12 seconds)

1.  $\frac{1}{\sqrt{3} + 1}$

2.  $\frac{1}{\sqrt{3} - 1}$

3.  $\frac{\sqrt{3} - 1}{2}$

4.  $\frac{\sqrt{3}}{\sqrt{3} - 1}$

A block of mass 0.02 kg is connected with spring and is free to oscillate on a horizontal smooth surface as shown. The angular frequency of oscillation is 2 rad ${\mathrm{s}}^{-1}$. The block is pulled by 4 cm (from equilibrium position) and then pushed towards the spring with a velocity of 8 cm/s. The amplitude of oscillation is (Neglect any damping)

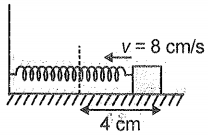
1.  $3\sqrt{2} \mathrm{cm}$

2.  $4\sqrt{2} \mathrm{cm}$

3.  $2\sqrt{2} \mathrm{cm}$

4.  1 cm

A particle moves on a circular path with uniform speed about the origin. The \((x-t)\) graph will be:
(\(x:\) value of \(x-\)coordinate; \(t-\)time)

1.		2.
3.		4.

A simple pendulum has time period \(T.\) The bob is given negative charge and surface below it is given a positive charge. The new time period will be:
1. less than \(T\)
2. greater than \(T\)
3. equal to \(T\)
4. infinite

A simple pendulum attached to the ceiling of a stationary lift has a time period of 1 s. The distance y covered by the lift moving downward varies with time as y = 3.75 ${\mathrm{t}}^2$, where y is in meters and t is in seconds. If g = 10 $\mathrm{m}/{\mathrm{s}}^2$, then the time period of the pendulum will be:

Which of the following may represent the potential energy of a body in S.H.M.? (Symbols have usual meaning)
1. ${\mathrm{m\omega }}^2{\mathrm{A}}^2$
2. $\frac{1}{2}{\mathrm{m\omega }}^2{\mathrm{X}}^2$
3. $\left(2{\mathrm{A}}^2 + \frac{1}{{\mathrm{m\omega }}^2}\right)$
4. both (2) and (3)

A particle moves according $\mathrm{x} = \left(6 \mathrm{cm}\right) \cos \left(\frac{\mathrm{\pi }}{2}\mathrm{t}\right)$. Average velocity of the particle in the time interval between t = 0 to t = 3 s is

1.  1 cm/s

2.  3.5 cm/s

3.  2 cm/s

4.  6 cm/s

A particle performs SHM with frequency \(f.\) The frequency of its velocity and acceleration are respectively:
1. \(f,~f\)
2. \(\frac{f}{2},~f\)
3. \(2f,~f\)
4. \(f,~2f\)