A particle is performing SHM with amplitude \(A\) and angular velocity \(\omega.\) The ratio of the magnitude of maximum velocity to maximum acceleration is:
1. \(\omega\)
2. \(\dfrac{1}{\omega }\)
3. \(\omega^{2} \)
4. \(A\omega\)

The potential energy of a particle executing SHM is 2.5 J when its displacement is half of the amplitude. The total energy of the particle is:

1.  18 J

2.  10 J

3.  12 J

4.  2.5 J

Choose the incorrect statement:

If a simple pendulum is suspended from the roof of a trolley which moves in the horizontal direction with an acceleration a, then the time period is given by $\mathrm{T} = 2\mathrm{\pi }\sqrt{\frac{\mathrm{l}}{\mathrm{g}\text{'}}}$, where $g\text{'}$ is equal to:

1.  g

2.  g - a

3.  g + a 

4.  $\sqrt{{\mathrm{g}}^2 + {\mathrm{a}}^2}$

In the given figure, when two identical springs are attached with a body of mass m, then oscillation frequency is f. If one spring is removed, then the frequency will become

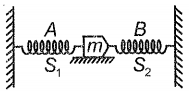
1.  f

2.  2f

3.  $\sqrt{2f}$

4.  $\frac{f}{\sqrt{2}}$

The function ${\sin }^2\left(\omega t\right)$ represents:

1.  An SHM with a period of $\frac{2\mathrm{\pi }}{\mathrm{\omega }}$

2.  An SHM with a period of $\frac{\mathrm{\pi }}{\mathrm{\omega }}$

3.  A periodic motion but not SHM with a period of $\frac{2\mathrm{\pi }}{\mathrm{\omega }}$

4.  A periodic motion but not SHM with a period of $\frac{\mathrm{\pi }}{\mathrm{\omega }}$

Values of the acceleration A of a particle moving in simple harmonic motion as a function of its displacement x are given below

$\mathbf{A}\mathbf{ }\mathbf{\left(}\mathbf{mms}{\mathbf{-}}^{\mathbf{2}}\mathbf{\right)}$      16   8   0   8   -16

x  (mm)                  4    -2   0   2     4

The period of the motion is :

1.  $\frac{1}{\mathrm{\pi }}\mathrm{s}$

2.  $\frac{2}{\mathrm{\pi }}\mathrm{s}$

3.  $\frac{\mathrm{\pi }}{2}s$

4.  $\mathrm{\pi s}$

The acceleration-time graph of a particle undergoing SHM is shown in the figure. Then,

A body of mass M is situated in a potential field. The potential energy of the body is given by $\mathrm{U}\left(\mathrm{x}\right) = {\mathrm{U}}_0\left[1 - \cos \mathrm{Kx}\right]$; where x is position, K and ${\mathrm{U}}_0$ are constant. Period of small oscillations of the body will be:

1.  $2\mathrm{\pi }\sqrt{{\mathrm{MU}}_0{\mathrm{K}}^2}$

2.  $2\mathrm{\pi }\sqrt{\frac{\mathrm{M}}{{\mathrm{U}}_0{\mathrm{K}}^2}}$

3.  $2\mathrm{\pi }\sqrt{\frac{{\mathrm{U}}_0{\mathrm{K}}^2}{\mathrm{M}}}$

4.  $2\mathrm{\pi }\sqrt{\frac{{\mathrm{U}}_0}{{\mathrm{MK}}^2}}$