Equation of simple harmonic motion of a particle is y = (0.4 m) sin314t, where time t is in second. Frequency of vibration of the particle is

1.  100 Hz

2.  75 Hz

3.  50 Hz

4.  25 Hz

A particle starts SHM from the mean position. Its amplitude is A and time period is T. At the time when its speed is half of its maximum speed, its displacement is

1.  $\frac{\mathrm{A}}{2}$

2.  $\frac{\mathrm{A}}{\sqrt{2}}$

3.  $\frac{\mathrm{A}\sqrt{3}}{2}$

4.  $\frac{2\mathrm{A}}{\sqrt{3}}$

A particle is performing SHM with amplitude \(A\) and angular velocity \(\omega.\) The ratio of the magnitude of maximum velocity to maximum acceleration is:
1. \(\omega\)
2. \(\dfrac{1}{\omega }\)
3. \(\omega^{2} \)
4. \(A\omega\)

The potential energy of a particle executing SHM is 2.5 J when its displacement is half of the amplitude. The total energy of the particle is:

1.  18 J

2.  10 J

3.  12 J

4.  2.5 J

Choose the incorrect statement:

If a simple pendulum is suspended from the roof of a trolley which moves in the horizontal direction with an acceleration a, then the time period is given by $\mathrm{T} = 2\mathrm{\pi }\sqrt{\frac{\mathrm{l}}{\mathrm{g}\text{'}}}$, where $g\text{'}$ is equal to:

1.  g

2.  g - a

3.  g + a 

4.  $\sqrt{{\mathrm{g}}^2 + {\mathrm{a}}^2}$

In the given figure, when two identical springs are attached with a body of mass m, then oscillation frequency is f. If one spring is removed, then the frequency will become

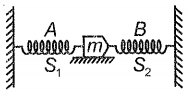
1.  f

2.  2f

3.  $\sqrt{2f}$

4.  $\frac{f}{\sqrt{2}}$

The function ${\sin }^2\left(\omega t\right)$ represents:

1.  An SHM with a period of $\frac{2\mathrm{\pi }}{\mathrm{\omega }}$

2.  An SHM with a period of $\frac{\mathrm{\pi }}{\mathrm{\omega }}$

3.  A periodic motion but not SHM with a period of $\frac{2\mathrm{\pi }}{\mathrm{\omega }}$

4.  A periodic motion but not SHM with a period of $\frac{\mathrm{\pi }}{\mathrm{\omega }}$