The amplitude of a simple harmonic oscillator is A and speed at the mean position is ${\mathrm{v}}_0$. The speed of the oscillator at the position $\mathrm{x} = \frac{\mathrm{A}}{\sqrt{3}}$ is:

1.  $\frac{2v_0}{\sqrt{3}}$

2.  $\frac{\sqrt{2}{v}_0}{3}$

3.  $\frac{2}{3}{v}_0$

4.  $\frac{\sqrt{2}{v}_0}{\sqrt{3}}$

The initial phase of the particle executing SHM with y = 4 sin $\mathrm{\omega }$t + 3 cos $\mathrm{\omega }$t is 

1.  53°

2.  37° 

3.  90°

4.  45°

A spring-block system is brought from the Earth's surface to deep inside the mine. Its period of oscillation will:

A particle executes S.H.M with amplitude A. If the time taken by the particle to travel from -A to A/2 is 4 seconds, its time period is 

1.  4s

2.  8s 

3.  12 s

4.  18 s

Two simple harmonic motions are represented by ${\mathrm{y}}_1 = 6 \sin \left(2\mathrm{\pi t} + \frac{\mathrm{\pi }}{3}\right)$ and ${\mathrm{y}}_2 = 3\left(\sin 2\mathrm{\pi t} + \cos 2\mathrm{\pi t}\right)$. The ratio of their amplitudes is

1.  $\sqrt{2}$

2.  $\frac{2}{3}$

3.  $\frac{1}{2}$

4.  $2\sqrt{2}$

A disc executes S.H.M. about the axis XX' in the plane of the disc as shown in the figure. Its time period of oscillation is:

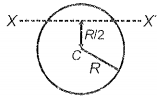
1.  $\mathrm{\pi }\sqrt{\frac{6\mathrm{R}}{\mathrm{g}}}$

2.  $2\mathrm{\pi }\sqrt{\frac{\mathrm{R}}{\mathrm{g}}}$

3.  $2\mathrm{\pi }\sqrt{\frac{2\mathrm{R}}{\mathrm{g}}}$

4.  $\mathrm{\pi }\sqrt{\frac{3\mathrm{R}}{2\mathrm{g}}}$

A spring-block system shown in the figure oscillates with a certain time period. If charge \(q\) is given to the block and a uniform field \(E\) is switched on, then its time period of oscillation is:

The period of oscillation of the spring block system shown in the figure is: (assume pulleys and spring to be ideal)

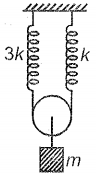
1.  $2\mathrm{\pi }\sqrt{\frac{\mathrm{m}}{3\mathrm{k}}}$

2.  $2\mathrm{\pi }\sqrt{\frac{4\mathrm{m}}{3\mathrm{k}}}$

3.  $2\mathrm{\pi }\sqrt{\frac{3\mathrm{m}}{4\mathrm{k}}}$

4.  $2\mathrm{\pi }\sqrt{\frac{\mathrm{m}}{\mathrm{k}}}$

The graph between velocity and acceleration of a particle executing S.H.M. can be

1.  A circle

2.  An ellipse

3.  A straight line

4.  Both (1) & (2)

The potential energy of a particle of mass m executing SHM is given by U = A(1 - cos2x), where x is the instantaneous displacement of the particle. The time period of oscillation is

1.  $\mathrm{\pi }\sqrt{\frac{\mathrm{m}}{\mathrm{A}}}$

2.  $2\mathrm{\pi }\sqrt{\frac{\mathrm{m}}{\mathrm{A}}}$

3.  $\mathrm{\pi }\sqrt{\frac{\mathrm{m}}{2\mathrm{A}}}$

4.  $2\mathrm{\pi }\sqrt{\frac{\mathrm{m}}{2\mathrm{A}}}$