The period of oscillation of the spring block system shown in the figure is: (assume pulleys and spring to be ideal)

                    

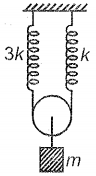
1.  $2\mathrm{\pi }\sqrt{\frac{\mathrm{m}}{3\mathrm{k}}}$

2.  $2\mathrm{\pi }\sqrt{\frac{4\mathrm{m}}{3\mathrm{k}}}$

3.  $2\mathrm{\pi }\sqrt{\frac{3\mathrm{m}}{4\mathrm{k}}}$

4.  $2\mathrm{\pi }\sqrt{\frac{\mathrm{m}}{\mathrm{k}}}$

The graph between velocity and acceleration of a particle executing S.H.M. can be

1.  A circle

2.  An ellipse

3.  A straight line

4.  Both (1) & (2)

The potential energy of a particle of mass m executing SHM is given by U = A(1 - cos2x), where x is the instantaneous displacement of the particle. The time period of oscillation is

1.  $\mathrm{\pi }\sqrt{\frac{\mathrm{m}}{\mathrm{A}}}$

2.  $2\mathrm{\pi }\sqrt{\frac{\mathrm{m}}{\mathrm{A}}}$

3.  $\mathrm{\pi }\sqrt{\frac{\mathrm{m}}{2\mathrm{A}}}$

4.  $2\mathrm{\pi }\sqrt{\frac{\mathrm{m}}{2\mathrm{A}}}$

A uniform rod of length l is suspended at $\frac{\mathrm{l}}{4}$ from one end and made to undergo small oscillations. The time period of oscillation is:

1.  $2\mathrm{\pi }\sqrt{\frac{7l}{12\mathrm{g}}}$

2.  $2\mathrm{\pi }\sqrt{\frac{3l}{7\mathrm{g}}}$

3.  $2\mathrm{\pi }\sqrt{\frac{7l}{3\mathrm{g}}}$

4.  $2\mathrm{\pi }\sqrt{\frac{4l}{5\mathrm{g}}}$

A simple pendulum with a metallic bob has a time period T. The bob is now immersed in a nonviscous liquid and the time period is found to be $\sqrt{5}$T. The ratio of the density of the metal to that of liquid is 

1.  1/4

2.  4/3

3.  5/4

4.  7/3

A particle executes SHM with time period \(T\). The time period of oscillation of total energy is:
1. \(T\)
2. \(2T\)
3. \(\dfrac{T}{2}\)
4. Infinite

A particle is executing linear simple harmonic motion with an amplitude \(a\) and an angular frequency \(\omega.\) Its average speed for its motion from extreme to mean position will be:
1. \(\frac{a\omega}{4}\)
2. \(\frac{a\omega}{2\pi}\)
3. \(\frac{2a\omega}{\pi}\)
4. \(\frac{a\omega}{\sqrt{3}\pi}\)

The time period of oscillation of a simple pendulum of length equal to half of the diameter of the earth is about 

1.  60 minute

2.  84.6 minute

3.  42.3 minute

4.  24 hour

The time period of the given spring-mass system is:

The equation of simple harmonic motion is given by X = (4 cm)$\sin \left(6.28 t + \frac{5\mathrm{\pi }}{3}\right)$, then maximum velocity of the particle in simple harmonic motion is: 

1.  25.12 m/s 

2.  25.12 cm/s 

3.  12.56 m/s 

4.  12.56 cm/s