Two simple harmonic motions are represented by ${\mathrm{y}}_1 = 6 \sin \left(2\mathrm{\pi t} + \frac{\mathrm{\pi }}{3}\right)$ and ${\mathrm{y}}_2 = 3\left(\sin 2\mathrm{\pi t} + \cos 2\mathrm{\pi t}\right)$. The ratio of their amplitudes is

1.  $\sqrt{2}$

2.  $\frac{2}{3}$

3.  $\frac{1}{2}$

4.  $2\sqrt{2}$

A disc executes S.H.M. about the axis XX' in the plane of the disc as shown in the figure. Its time period of oscillation is:

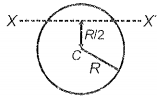
1.  $\mathrm{\pi }\sqrt{\frac{6\mathrm{R}}{\mathrm{g}}}$

2.  $2\mathrm{\pi }\sqrt{\frac{\mathrm{R}}{\mathrm{g}}}$

3.  $2\mathrm{\pi }\sqrt{\frac{2\mathrm{R}}{\mathrm{g}}}$

4.  $\mathrm{\pi }\sqrt{\frac{3\mathrm{R}}{2\mathrm{g}}}$

A spring-block system shown in the figure oscillates with a certain time period. If charge \(q\) is given to the block and a uniform field \(E\) is switched on, then its time period of oscillation is:

The period of oscillation of the spring block system shown in the figure is: (assume pulleys and spring to be ideal)

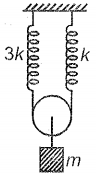
1.  $2\mathrm{\pi }\sqrt{\frac{\mathrm{m}}{3\mathrm{k}}}$

2.  $2\mathrm{\pi }\sqrt{\frac{4\mathrm{m}}{3\mathrm{k}}}$

3.  $2\mathrm{\pi }\sqrt{\frac{3\mathrm{m}}{4\mathrm{k}}}$

4.  $2\mathrm{\pi }\sqrt{\frac{\mathrm{m}}{\mathrm{k}}}$

The graph between velocity and acceleration of a particle executing S.H.M. can be

1.  A circle

2.  An ellipse

3.  A straight line

4.  Both (1) & (2)

The potential energy of a particle of mass m executing SHM is given by U = A(1 - cos2x), where x is the instantaneous displacement of the particle. The time period of oscillation is

1.  $\mathrm{\pi }\sqrt{\frac{\mathrm{m}}{\mathrm{A}}}$

2.  $2\mathrm{\pi }\sqrt{\frac{\mathrm{m}}{\mathrm{A}}}$

3.  $\mathrm{\pi }\sqrt{\frac{\mathrm{m}}{2\mathrm{A}}}$

4.  $2\mathrm{\pi }\sqrt{\frac{\mathrm{m}}{2\mathrm{A}}}$

A uniform rod of length l is suspended at $\frac{\mathrm{l}}{4}$ from one end and made to undergo small oscillations. The time period of oscillation is:

1.  $2\mathrm{\pi }\sqrt{\frac{7l}{12\mathrm{g}}}$

2.  $2\mathrm{\pi }\sqrt{\frac{3l}{7\mathrm{g}}}$

3.  $2\mathrm{\pi }\sqrt{\frac{7l}{3\mathrm{g}}}$

4.  $2\mathrm{\pi }\sqrt{\frac{4l}{5\mathrm{g}}}$

A simple pendulum with a metallic bob has a time period T. The bob is now immersed in a nonviscous liquid and the time period is found to be $\sqrt{5}$T. The ratio of the density of the metal to that of liquid is 

1.  1/4

2.  4/3

3.  5/4

4.  7/3

A particle executes SHM with time period \(T\). The time period of oscillation of total energy is:
1. \(T\)
2. \(2T\)
3. \(\dfrac{T}{2}\)
4. Infinite

A particle is executing linear simple harmonic motion with an amplitude \(a\) and an angular frequency \(\omega.\) Its average speed for its motion from extreme to mean position will be:
1. \(\frac{a\omega}{4}\)
2. \(\frac{a\omega}{2\pi}\)
3. \(\frac{2a\omega}{\pi}\)
4. \(\frac{a\omega}{\sqrt{3}\pi}\)