The time period of vibration of a uniform disc of mass 'M' and radius 'R' about an axis perpendicular to the plane of disc and passing from a point at a distance from the center of the disc is:
1.
2.
3.
4.
Two identical blocks each of mass 'M' are connected with springs of spring constant K and placed on a smooth surface as shown in the figure. When the blocks are in contact the springs are in its natural length. The collision between the masses is elastic. The frequency of vibration on disturbing the masses symmetrically in the directions of arrows and releasing them is
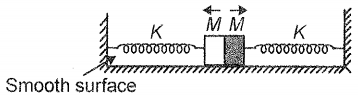
1.
2.
3.
4.
Two mutually perpendicular simple harmonic vibrations of the same frequency superimpose on each other. The amplitude of the two vibrations is different and they are different from each other in phase. The resultant of superposition is
1. Parabola
2. Straight line
3. Elliptical
4. Circular
1. \(0^\circ\)
2. \(\alpha^\circ\)
3. \(90^\circ\)
4. \(180^\circ\)
A ring of radius R is hung by a nail on its periphery such that it can freely rotate in its vertical plane. The time period of the ring for small oscillations is:
1.
2.
3.
4.
| 1. | Zero | 2. | \(30~\text{J}\) |
| 3. | \(20~\text{J}\) | 4. | \(40~\text{J}\) |
The equation of S.H.M. is given as x = Asin(0.02), where t is in seconds. With what time period the potential energy oscillates?
1. 200 s
2. 100 s
3. 50 s
4. 10 s
In a stationary lift, a spring-block system oscillates with a frequency \(f.\) When the lift accelerates, the frequency becomes \(f'\) . Then:
| 1. | \(f'>f\) |
| 2. | \(f'<f\) |
| 3. | \(f'=f\) |
| 4. | any of the above depending on the value of the acceleration of the lift. |

1. \(\frac{\pi}{2}~\text{s}\)
2. \(\frac{1}{2}~\text{s}\)
3. \(\pi~\text{s}\)
4. \(1~\text{s}\)
| 1. | \(3~\text{cm}\) | 2. | \(3.5~\text{cm}\) |
| 3. | \(4~\text{cm}\) | 4. | \(5~\text{cm}\) |






