Ten electrons are equally spaced and fixed around a circle of radius \(R\). Relative to \(V=0\) at infinity, the electrostatic potential \(V\) and the electric field \(E\) at the centre \(C\) are:

1.	\(V \neq 0 \text { and } \vec{E} \neq 0\)
2.	\(V \neq 0 \text { and } \vec{E}=0\)
3.	\(V=0 \text { and } \vec{E}=0\)
4.	\(V=0 \text { and } \vec{E} \neq 0\)

The displacement of a charge Q in the electric field $E=e_1\hat{i}+e_2\hat{j}+e_3\hat{k}$ is $\hat{r}=a\hat{i}+b\hat{j}$. The work done is 

1. $Q(a{e}_1+b{e}_2)$

2. $Q\sqrt{{\left(a{e}_1\right)}^2+{\left(b{e}_2\right)}^2}$

3. $Q(e_1+e_2)\sqrt{a^2+b^2}$

4. $Q\left(\sqrt{e_1^2+e_2^2)}\right(a+b)$

Three charges Q, +q and +q are placed at the vertices of a right-angled isosceles triangle as shown. The net electrostatic energy of the configuration is zero if Q is equal to

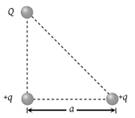
1. $\frac{-q}{1+\sqrt{2}}$

2. $\frac{-2q}{2+\sqrt{2}}$

3. –2q

4. +q

Three charges \(Q\), \(+q \) and \(+q \) are placed at the vertices of an equilateral triangle of side \(l\) as shown in the figure. If the net electrostatic energy of the system is zero, then \(Q\) is equal to:

Electric potential at any point is $V=-5x+3y+\sqrt{15}z$, then the magnitude of the electric field is

1. $3\sqrt{2}$

2. $4\sqrt{2}$

3. $5\sqrt{2}$

4. 7

Kinetic energy of an electron accelerated in a potential difference of 100 V is 

1. 1.6 × 10^–17 J

2. 1.6 × 10²¹ J

3. 1.6 × 10^–29 J

4. 1.6 × 10^–34 J

If identical charges (–q) are placed at each corner of a cube of side b, then electric potential energy of charge (+q) which is placed at centre of the cube will be -

1. $\frac{8\sqrt{2}{q}^2}{4\pi {\epsilon }_{0}b}$

2. $\frac{-8\sqrt{2}{q}^2}{\pi {\epsilon }_{0}b}$

3. $\frac{-4\sqrt{2}{q}^2}{\pi {\epsilon }_{0}b}$

4. $\frac{-4q^2}{\sqrt{3}\pi {\epsilon }_{0}b}$

A proton is about 1840 times heavier than an electron. When it is accelerated by a potential difference of 1 kV, its kinetic energy will be -

1. 1840 keV

2. 1/1840 keV

3. 1 keV

4. 920 keV

A thin spherical conducting shell of radius \(R\) has a charge \(q.\) Another charge \(Q\) is placed at the centre of the shell. The electrostatic potential at a point \(P\) which is at a distance \(\frac{R}{2}\) from the centre of the shell is:
1. \(\frac{\left( q + Q \right)}{4 \pi \varepsilon_{0}} \frac{2}{R}\)
2. \(\frac{2 Q}{4 \pi \varepsilon_{0} R}\)
3. \(\frac{2 Q}{4 \pi \varepsilon_{0} R} - \frac{2 q}{4 \pi \varepsilon_{0} R}\)
4. \(\frac{2 Q}{4 \pi \varepsilon_{0} R} + \frac{q}{4 \pi \varepsilon_{0} R}\)