A simple pendulum attached to the ceiling of a stationary lift has a time period of 1 s. The distance y covered by the lift moving downward varies with time as y = 3.75 ${\mathrm{t}}^2$, where y is in meters and t is in seconds. If g = 10 $\mathrm{m}/{\mathrm{s}}^2$, then the time period of the pendulum will be:

1.	4 s	2.	6 s
3.	2 s	4.	12 s

Which of the following may represent the potential energy of a body in S.H.M.? (Symbols have usual meaning)
1. ${\mathrm{m\omega }}^2{\mathrm{A}}^2$
2. $\frac{1}{2}{\mathrm{m\omega }}^2{\mathrm{X}}^2$
3. $\left(2{\mathrm{A}}^2 + \frac{1}{{\mathrm{m\omega }}^2}\right)$
4. both (2) and (3)

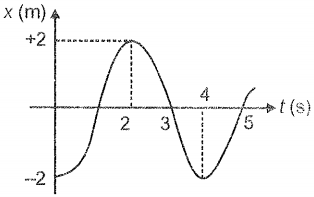
A particle moves according $\mathrm{x} = \left(6 \mathrm{cm}\right) \cos \left(\frac{\mathrm{\pi }}{2}\mathrm{t}\right)$. Average velocity of the particle in the time interval between t = 0 to t = 3 s is

1.  1 cm/s

2.  3.5 cm/s

3.  2 cm/s

4.  6 cm/s

A particle performs SHM with frequency \(f.\) The frequency of its velocity and acceleration are respectively:
1. \(f,~f\)
2. \(\frac{f}{2},~f\)
3. \(2f,~f\)
4. \(f,~2f\)

Force acting on a body free to move on the \(\mathrm{X}\)-axis is given by, \(F=-kx^n\) where \(k\) is a positive constant. For which value of \(n\) motion of the body is not oscillatory?

In a forced oscillation, when the system oscillates under the action of the driving force $\mathrm{F}$ $=$ ${\mathrm{F}}_0$ $\sin$ $\mathrm{\omega t}$ in addition to its internal restoring force, the particle oscillates with a frequency equal to

1.  The natural frequency of the body

2.  Frequency of driving force

3.  The difference in frequency of driving force and natural frequency

4.  Mean of the driving frequency and natural frequency

The  potential energy of a harmonic oscillator at equilibrium is 15 J and average kinetic energy is 5 J. Total energy at any instant is

1.  25 J

2.  5 J

3.  15 J

4.  40 J

A particle is executing S.H.M. Graph of its displacement with the position is shown in the figure. Maximum acceleration of the particle is

1.  $\frac{{\mathrm{\pi }}^2}{2}\mathrm{m}/{\mathrm{s}}^2$

2.  $\frac{{\mathrm{\pi }}^2}{4}\mathrm{m}/{\mathrm{s}}^2$

3.  $4{\mathrm{\pi }}^2{\mathrm{\pi }}^2\mathrm{m}/{\mathrm{s}}^2$

4.  $\frac{{\mathrm{\pi }}^2}{8}\mathrm{m}/{\mathrm{s}}^2$

A uniform spring has a force constant K. It is cut into two pieces of lengths ${\mathrm{l}}_1 \mathrm{and} {\mathrm{l}}_2$, such that ${\mathrm{l}}_1 = {\mathrm{nl}}_2$. Time period of oscillation of a mass m with spring of length ${\mathrm{l}}_1$ is

1.  $2\mathrm{\pi }\sqrt{\frac{\mathrm{m}\left(\mathrm{n} + 1\right)}{\mathrm{nk}}}$

2.  $2\mathrm{\pi }\sqrt{\frac{\mathrm{k}\left(\mathrm{n} + 1\right)}{\mathrm{m}}}$

3.  $2\mathrm{\pi }\sqrt{\frac{\mathrm{m}}{\mathrm{k}\left(\mathrm{n} + 1\right)}}$

4.  $2\mathrm{\pi }\sqrt{\frac{\mathrm{mn}}{\mathrm{k}\left(\mathrm{n} + 1\right)}}$

A body executes oscillations under the effect of a small damping force. If the amplitude of the body reduces by 50% in 6 minutes, then amplitude after the next 12 minutes will be [initial amplitude is ${\mathrm{A}}_0$] -

1.  $\frac{{\mathrm{A}}_0}{4}$

2.  $\frac{{\mathrm{A}}_0}{8}$

3.  $\frac{{\mathrm{A}}_0}{16}$

4.  $\frac{{\mathrm{A}}_0}{6}$