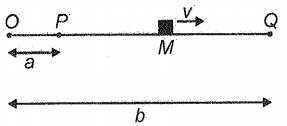
A particle performing S.H.M. is at rest at points P and Q which are at a distance a and b from point O. It has velocity v when it is halfway between P and Q. The time period of oscillation is:

                

1.  $\left[\frac{\mathrm{b} - \mathrm{a}}{\mathrm{b}\times \mathrm{a}}\right]\mathrm{v}$

2.  $\frac{\mathrm{\pi }\left(\mathrm{b} - \mathrm{a}\right)}{\mathrm{v}}$

3.  $\left(\frac{\mathrm{b} - \mathrm{a}}{\mathrm{ba}}\right)\mathrm{v}$

4.  Data is insufficient to answer.

The time period of a simple pendulum in a stationary lift is T. If the lift moves upwards with an acceleration g, then the new time period will be

1.  Infinite

2.  $\sqrt{0.6}\mathrm{T}$

3.  $\sqrt{1.67}\mathrm{T}$

4.  0.707T

Acceleration-time (\(a\text-t\)) graph for a particle performing SHM is shown in the figure. Select the incorrect statement.

A particle is executing S.H.M. such that its acceleration 'a' is a function of displacement x as $\mathrm{a} = -\mathrm{\beta }\left(\mathrm{x} - 6\right)$. The time period of the oscillation is

1.  $\frac{\mathrm{\pi }}{\mathrm{\beta }}$

2.  $\frac{\mathrm{\pi }}{2\mathrm{\beta }}$

3.  $\frac{2\mathrm{\pi }}{\sqrt{2}\mathrm{\beta }}$

4.  $\frac{2\mathrm{\pi }}{\sqrt{\mathrm{\beta }}}$

A particle of mass 0.5 kg is executing S.H.M. such that its potential energy is 5 J at the mean position. If its total mechanical energy is 9 J and the amplitude of oscillation is 1 cm, then the time period of oscillation of the particle is:

1.  $\frac{2\mathrm{\pi }}{100} \mathrm{s}$

2.  $\frac{\mathrm{\pi }}{200} \mathrm{s}$

3.  $\frac{2\mathrm{\pi }}{25} \mathrm{s}$

4.  $2\mathrm{\pi } \mathrm{s}$

The total mechanical energy of a linear harmonic oscillator is \(600\) J. At the mean position, its potential energy is \(100\) J. The minimum potential energy of the oscillator is: 
1. \(50\) J
2. \(500\) J
3. \(0\) 
4. \(100\) J

A general graph showing variation in the potential energy \((P.E)\) of a particle with time while executing S.H.M. is:

1.		2.
3.		4.

Two simple pendulums of lengths 1.44 m and 1 m start S.H.M. together in the same phase. They will be in the same phase again after

1.  6 vibrations of the longer pendulum

2.  6 vibrations of the smaller pendulum

3.  5 vibrations of the smaller pendulum

4.  4 vibrations of the longer pendulum

A spring has equilibrium elongation 0.1 m when suspended vertically with a load. If the load is slightly displaced vertically downward and released, then the time period of SHM of the system will be approximately

1.  0.1 s

2.  0.4 s

3.  0.6 s

4.  0.3

Select the correct statements regarding potential energy \((U)\) in the simple harmonic motion of a particle along \(x\text-\)axis: