Acceleration-time (\(a\text-t\)) graph for a particle performing SHM is shown in the figure. Select the incorrect statement.

             

1.	Displacement of a particle at \(A\) is negative.
2.	The potential energy of the particle at \(C\) is minimum.
3.	The velocity of the particle at \(B\) is positive.
4.	Speed of particle at \(D\) is decreasing.

A particle is executing S.H.M. such that its acceleration 'a' is a function of displacement x as $\mathrm{a} = -\mathrm{\beta }\left(\mathrm{x} - 6\right)$. The time period of the oscillation is

1.  $\frac{\mathrm{\pi }}{\mathrm{\beta }}$

2.  $\frac{\mathrm{\pi }}{2\mathrm{\beta }}$

3.  $\frac{2\mathrm{\pi }}{\sqrt{2}\mathrm{\beta }}$

4.  $\frac{2\mathrm{\pi }}{\sqrt{\mathrm{\beta }}}$

A particle of mass 0.5 kg is executing S.H.M. such that its potential energy is 5 J at the mean position. If its total mechanical energy is 9 J and the amplitude of oscillation is 1 cm, then the time period of oscillation of the particle is:

1.  $\frac{2\mathrm{\pi }}{100} \mathrm{s}$

2.  $\frac{\mathrm{\pi }}{200} \mathrm{s}$

3.  $\frac{2\mathrm{\pi }}{25} \mathrm{s}$

4.  $2\mathrm{\pi } \mathrm{s}$

The total mechanical energy of a linear harmonic oscillator is \(600\) J. At the mean position, its potential energy is \(100\) J. The minimum potential energy of the oscillator is: 
1. \(50\) J
2. \(500\) J
3. \(0\) 
4. \(100\) J

A general graph showing variation in the potential energy \((P.E)\) of a particle with time while executing S.H.M. is:

1.		2.
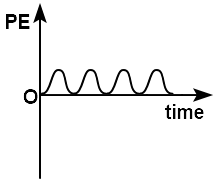3.		4.

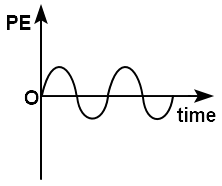Two simple pendulums of lengths 1.44 m and 1 m start S.H.M. together in the same phase. They will be in the same phase again after

1.  6 vibrations of the longer pendulum

2.  6 vibrations of the smaller pendulum

3.  5 vibrations of the smaller pendulum

4.  4 vibrations of the longer pendulum

A spring has equilibrium elongation 0.1 m when suspended vertically with a load. If the load is slightly displaced vertically downward and released, then the time period of SHM of the system will be approximately

1.  0.1 s

2.  0.4 s

3.  0.6 s

4.  0.3

Select the correct statements regarding potential energy \((U)\) in the simple harmonic motion of a particle along \(x\text-\)axis:

A simple pendulum is pushed slightly from its equilibrium towards the left and then set free to execute the simple harmonic motion. Select the correct graph between its velocity (\(v\)) and displacement (\(x \)).

1.		2.
3.		4.

Simple harmonic motion is an example of: