The displacement of a body performing simple harmonic motion is represented by $\mathrm{x} = \mathrm{asin}\left(2\mathrm{\pi t} + \frac{\mathrm{\pi }}{3}\right)$. After what approximate time from t = 0, the speed of the particle becomes maximum for the first time?

1.  0.12 s

2.  0.24 s

3.  0.33 s

4.  0.42 s

A particle is performing S.H.M. with a time period 8 s and starts from the origin. The ratio of distance travelled by a particle in 1st second and 2nd second of its motion is :

1.  $\sqrt{2}$

2.  ($\sqrt{2}$ + 1)

3.  ($\sqrt{2}$ - 1)

4.  2

Two particles are executing SHM about the same mean position, along the same straight line, with the same amplitude and time period. At any instant, they meet each other at, \(\frac{-A}{2}\) while moving in the opposite direction. The phase difference between them is:
1. \(\frac{2\pi}{3}\)
2. \(\frac{\pi}{3}\)
3. \(\frac{11\pi}{6}\)
4. \(\frac{7\pi}{6}\)

A small block of mass m is kept on a wooden plank which is oscillating in the vertical plane (as shown), with time period T. The amplitude of oscillation at which block leaves contact with the plank is

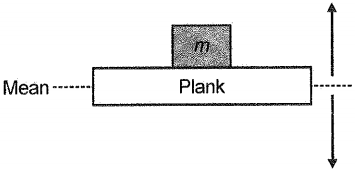
1.  $\ge \frac{{\mathrm{gT}}^2}{4\mathrm{\pi }}$

2.  $\le \frac{{\mathrm{gT}}^2}{4\mathrm{\pi }}$

3.  $\ge \frac{{\mathrm{gT}}^2}{4{\mathrm{\pi }}^2}$

4.  $\le \frac{{\mathrm{gT}}^2}{4{\mathrm{\pi }}^2}$

A particle performing S.H.M. is at rest at points P and Q which are at a distance a and b from point O. It has velocity v when it is halfway between P and Q. The time period of oscillation is:

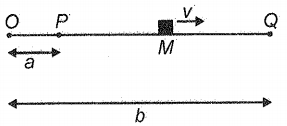
1.  $\left[\frac{\mathrm{b} - \mathrm{a}}{\mathrm{b}\times \mathrm{a}}\right]\mathrm{v}$

2.  $\frac{\mathrm{\pi }\left(\mathrm{b} - \mathrm{a}\right)}{\mathrm{v}}$

3.  $\left(\frac{\mathrm{b} - \mathrm{a}}{\mathrm{ba}}\right)\mathrm{v}$

4.  Data is insufficient to answer.

The time period of a simple pendulum in a stationary lift is T. If the lift moves upwards with an acceleration g, then the new time period will be

1.  Infinite

2.  $\sqrt{0.6}\mathrm{T}$

3.  $\sqrt{1.67}\mathrm{T}$

4.  0.707T

Acceleration-time (\(a\text-t\)) graph for a particle performing SHM is shown in the figure. Select the incorrect statement.

A particle is executing S.H.M. such that its acceleration 'a' is a function of displacement x as $\mathrm{a} = -\mathrm{\beta }\left(\mathrm{x} - 6\right)$. The time period of the oscillation is

1.  $\frac{\mathrm{\pi }}{\mathrm{\beta }}$

2.  $\frac{\mathrm{\pi }}{2\mathrm{\beta }}$

3.  $\frac{2\mathrm{\pi }}{\sqrt{2}\mathrm{\beta }}$

4.  $\frac{2\mathrm{\pi }}{\sqrt{\mathrm{\beta }}}$

A particle of mass 0.5 kg is executing S.H.M. such that its potential energy is 5 J at the mean position. If its total mechanical energy is 9 J and the amplitude of oscillation is 1 cm, then the time period of oscillation of the particle is:

1.  $\frac{2\mathrm{\pi }}{100} \mathrm{s}$

2.  $\frac{\mathrm{\pi }}{200} \mathrm{s}$

3.  $\frac{2\mathrm{\pi }}{25} \mathrm{s}$

4.  $2\mathrm{\pi } \mathrm{s}$

The total mechanical energy of a linear harmonic oscillator is \(600\) J. At the mean position, its potential energy is \(100\) J. The minimum potential energy of the oscillator is: 
1. \(50\) J
2. \(500\) J
3. \(0\) 
4. \(100\) J