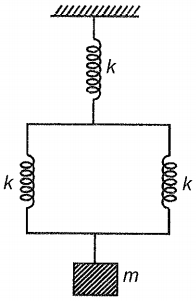
A body of mass m hanging with the help of three springs, each of spring constant k as shown. If the mass is slightly displaced and released, then the system will oscillate with the time period

                     

1.  $2\mathrm{\pi }\sqrt{\frac{\mathrm{m}}{3\mathrm{k}}}$

2.  $2\mathrm{\pi }\sqrt{\frac{2\mathrm{m}}{3\mathrm{k}}}$

3.  $2\mathrm{\pi }\sqrt{\frac{3\mathrm{m}}{2\mathrm{k}}}$

4.  $2\mathrm{\pi }\sqrt{\frac{3\mathrm{m}}{\mathrm{k}}}$

A block of mass m attached to a spring of constant k oscillates on a smooth surface. The other end of the spring is fixed to a wall. When spring is at its natural length, the speed of the block is v. Displacement of the block from its mean position before coming to instantaneous rest is:

1.  $\sqrt{\frac{\mathrm{mv}}{\mathrm{k}}}$

2.  $\mathrm{v}\sqrt{\frac{\mathrm{m}}{\mathrm{k}}}$

3.  $\mathrm{m}\sqrt{\frac{\mathrm{v}}{\mathrm{k}}}$

4.  $\frac{1}{\mathrm{k}}\sqrt{\frac{\mathrm{m}}{\mathrm{v}}}$

A particle under SHM has a maximum speed of 30 cm/s and a maximum acceleration of 60 cm/s? The time period of oscillation (in second) is

1.  $\frac{\mathrm{\pi }}{2}$

2.  2$\mathrm{\pi }$

3.  $\mathrm{\pi }$

4.  4$\mathrm{\pi }$

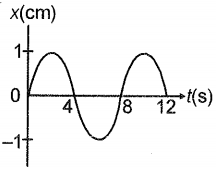
The x-t graph of a particle undergoing SHM is shown below. The acceleration of the particle at $\mathrm{t} = \frac{4}{3}$ is:

1.  $\frac{\sqrt{3}}{32}{\mathrm{\pi }}^3 \mathrm{cm}/{\mathrm{s}}^2$

2.  $-\frac{{\mathrm{\pi }}^2}{32} \mathrm{cm}/{\mathrm{s}}^2$

3.  $\frac{{\mathrm{\pi }}^2}{32} \mathrm{cm}/{\mathrm{s}}^2$

4.  $-\frac{\sqrt{3}}{32}{\mathrm{\pi }}^2 \mathrm{cm}/{\mathrm{s}}^2$

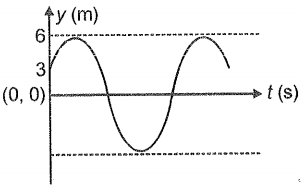
The position-time (y - t) graph of a particle executing S.H.M. is shown. The time period of the particle is 4 seconds. Equation of particle executing S.H.M. is

1.  $\mathrm{y} = 6 \sin \left(2\mathrm{\pi t} + \frac{\mathrm{\pi }}{6}\right)$

2.  $\mathrm{y} = 6 \sin \left(\frac{\mathrm{\pi }}{2}\mathrm{t} + \frac{\mathrm{\pi }}{3}\right)$

3.  $\mathrm{y} = 6 \sin \left(\frac{\mathrm{\pi }}{2}\mathrm{t} + \frac{\mathrm{\pi }}{6}\right)$

4.  $\mathrm{y} = 6 \sin \left(\frac{\mathrm{\pi }}{2}\mathrm{t} - \frac{\mathrm{\pi }}{6}\right)$

A particle starts executing SHM from an extreme position with time period T and amplitude A. The distance travelled by the particle in time $\frac{15\mathrm{T}}{18}$is:

1.  3.5 A

2.  2.5 A

3.  0.5 A

4.  1.5

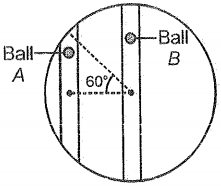
Two tunnels are dug across the earth as shown in the figure. Balls A and B are dropped in the tunnels. If the time period of oscillation of ball A is T, the time period of the oscillation of ball B is :

1.  T

2.  $\frac{\sqrt{3}}{2}\mathrm{T}$

3.  $\frac{2}{\sqrt{3}}\mathrm{T}$

4.  $\frac{2}{3}\mathrm{T}$

Select the correct statement(s) regarding S.H.M.

1.  The average speed of particle executing S.H.M. is zero in one complete oscillation.

2.  The graph between the kinetic and potential energy of a particle executing S.H.M. is a straight line.

3.  Restoring force acting on the particle is directed towards a fixed point and is directly proportional to the displacement from the mean position of the particle.

4.  Both (2) & (3)

The graph between the velocity \((v)\) of a particle executing SHM and its displacement \((x)\) is shown in the figure. The time period of oscillation for this SHM will be:

      
1. \(\sqrt{\frac{\alpha}{\beta}}\)
2. \(2\pi\sqrt{\frac{\alpha}{\beta}}\)
3. \(2\pi\left(\frac{\beta}{\alpha}\right)\)
4. \(2\pi\left(\frac{\alpha}{\beta}\right)\)

The displacement of a body performing simple harmonic motion is represented by $\mathrm{x} = \mathrm{asin}\left(2\mathrm{\pi t} + \frac{\mathrm{\pi }}{3}\right)$. After what approximate time from t = 0, the speed of the particle becomes maximum for the first time?

1.  0.12 s

2.  0.24 s

3.  0.33 s

4.  0.42 s