The oscillation of a body on a smooth horizontal surface is represented by the equation, \(X=A \text{cos}(\omega t)\),
where \(X=\) displacement at time \(t,\) \(\omega=\) frequency of oscillation.
Which one of the following graphs correctly shows the variation of acceleration, \(a\) with time, \(t?\)
(\(T=\) time period) \(a~~O~~T~~t~~\)
1.

2.

3.

4.

where \(X=\) displacement at time \(t,\) \(\omega=\) frequency of oscillation.
Which one of the following graphs correctly shows the variation of acceleration, \(a\) with time, \(t?\)
(\(T=\) time period) \(a~~O~~T~~t~~\)




1. Only (IV) does not represent SHM
2. (I) and (III)
3. (I) and (II)
4. Only (I)
A particle of mass \(m\) is released from rest and follows a parabolic path as shown. Assuming that the displacement of the mass from the origin is small, which graph correctly depicts the position of the particle as a function of time?
| 1. |  |
2. |  |
| 3. | 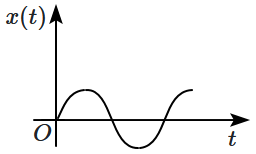 |
4. |  |
1. \(\frac{\pi a\sqrt3}{2T}\)
2. \(\frac{\pi a}{T}\)
3. \(\frac{3\pi^2 a}{T}\)
4. \(\frac{\pi a\sqrt3}{T}\)
1. Acceleration = -k0x + k1x2
2. Acceleration = -k(x+a)
3. Acceleration = k(x+a)
4. Acceleration = kx
1. 1: 10
2. 1: 102
3. 1: 103
4. 1: 104
Two points are located at a distance of \(10\) m and \(15\) m from the source of oscillation. The period of oscillation is \(0.05\) s and the velocity of the wave is \(300\) m/s. What is the phase difference between the oscillations of two points?
1. \(\frac{\pi}{3}\)
2. \(\frac{2\pi}{3}\)
3. \(\pi\)
4. \(\frac{\pi}{6}\)
A particle executes simple harmonic oscillation with an amplitude a. The period of oscillation is T. The minimum time taken by the particle to travel half of the amplitude from the equilibrium position is:
1.
2.
3.
4.
1. \(0~\text{and}~2K_0\)
2. \(\frac{K_0}{2}~\text{and}~K_0\)
3. \(K_0~\text{and}~2K_0\)
4. \(K_0~\text{and}~K_0\)
A mass of \(2.0\) kg is put on a flat pan attached to a vertical spring fixed on the ground as shown in the figure. The mass of the spring and the pan is negligible. When pressed slightly and released, the mass executes a simple harmonic motion. The spring constant is \(200\) N/m. What should be the minimum amplitude of the motion, so that the mass gets detached from the pan?
(Take \(g=10\) m/s2)
| 1. | \(8.0\) cm |
| 2. | \(10.0\) cm |
| 3. | any value less than \(12.0\) cm |
| 4. | \(4.0\) cm |




