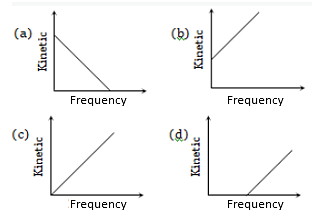
According to Einstein's photoelectric equation, the graph between the kinetic energy of photoelectrons ejected and the frequency of incident radiation is

For the photoelectric effect, the maximum kinetic energy ${\mathrm{E}}_1$ of the emitted photoelectrons is plotted against the frequency v of the incident photons as shown in the figure. The slope of the curve gives

(a) Charge of the electron

(b) Work function of the metal

(c) Planck's constant

(d) Ratio of the Planck’s constant to electronic charge

The stopping potential \(V\) for photoelectric emission from a metal surface is plotted along the \(Y\text-\)axis and the frequency \(\nu\) of incident light along the \(X\text-\)axis. A straight line is obtained as shown in the figure. Planck's constant is given by:
             

In an experiment on the photoelectric effect, the frequency \(f\) of the incident light is plotted against the stopping potential \(V_0.\) The work function of the photoelectric surface is given by:
(\(e\) is an electronic charge) 

The stopping potential as a function of the frequency of the incident radiation is plotted for two different photoelectric surfaces \(A\) and \(B\). The graphs demonstrate that \(A\)'s work function is:

The value of stopping potential in the following diagram is given by:
    

In the following diagram if ${\mathrm{V}}_2>{\mathrm{V}}_1$, then,

(1) ${\mathrm{\lambda }}_1=\sqrt{{\mathrm{\lambda }}_2}$

(2) ${\mathrm{\lambda }}_1<{\mathrm{\lambda }}_2$

(3) ${\mathrm{\lambda }}_1={\mathrm{\lambda }}_2$

(4) ${\mathrm{\lambda }}_1>{\mathrm{\lambda }}_2$