If a charged spherical conductor of radius 10 cm has potential V at a point distant 5 cm from its centre, then the potential at a point distant 15 cm from the centre will be -

1. $\frac{1}{3}V$

2. $\frac{2}{3}V$

3. $\frac{3}{2}V$

4. 3 V

An oil drop having charge 2e is kept stationary between two parallel horizontal plates 2.0 cm apart when a potential difference of 12000 volts is applied between them. If the density of oil is 900 kg/m³, the radius of the drop will be -

1. $2.0\times {10}^{-6}m$

2. $1.7\times {10}^{-6}m$

3. $1.4\times {10}^{-6}m$

4. $1.1\times {10}^{-6}m$

The ratio of momenta of an electron and an $\alpha$-particle which are accelerated from rest by a potential difference of 100 volt is 

1. 1

2. $\sqrt{\frac{2m_e}{m_{\alpha }}}$

3. $\sqrt{\frac{m_e}{m_{\alpha }}}$

4. $\sqrt{\frac{m_e}{2m_{\alpha }}}$

When a proton is accelerated through 1V, then its kinetic energy will be -

1. 1840 eV

2. 13.6 eV

3. 1 eV

4. 0.54 eV

The displacement of a charge Q in the electric field $E=e_1\hat{i}+e_2\hat{j}+e_3\hat{k}$ is $\hat{r}=a\hat{i}+b\hat{j}$. The work done is 

1. $Q(a{e}_1+b{e}_2)$

2. $Q\sqrt{{\left(a{e}_1\right)}^2+{\left(b{e}_2\right)}^2}$

3. $Q(e_1+e_2)\sqrt{a^2+b^2}$

4. $Q\left(\sqrt{e_1^2+e_2^2)}\right(a+b)$

Three charges Q, +q and +q are placed at the vertices of a right-angled isosceles triangle as shown. The net electrostatic energy of the configuration is zero if Q is equal to

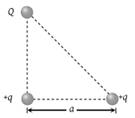
1. $\frac{-q}{1+\sqrt{2}}$

2. $\frac{-2q}{2+\sqrt{2}}$

3. –2q

4. +q

Three charges \(Q\), \(+q \) and \(+q \) are placed at the vertices of an equilateral triangle of side \(l\) as shown in the figure. If the net electrostatic energy of the system is zero, then \(Q\) is equal to: