A particle of mass m and charge q is placed at rest in a uniform electric field E and then released. The kinetic energy attained by the particle after moving a distance y is -

(1) $qE{y}^2$

(2) $q{E}^{2}y$

(3) $qEy$

(4) $q^{2}Ey$

How much kinetic energy will be gained by an $\alpha$– particle in going from a point at 70 V to another point at 50 V ?

(1) $40eV$

(2) $40keV$

(3) $40MeV$

(4) $0eV$

If a charged spherical conductor of radius 10 cm has potential V at a point distant 5 cm from its centre, then the potential at a point distant 15 cm from the centre will be -

(1) $\frac{1}{3}V$

(2) $\frac{2}{3}V$

(3) $\frac{3}{2}V$

(4) 3 V

An oil drop having charge 2e is kept stationary between two parallel horizontal plates 2.0 cm apart when a potential difference of 12000 volts is applied between them. If the density of oil is 900 kg/m³, the radius of the drop will be -

(1) $2.0\times {10}^{-6}m$

(2) $1.7\times {10}^{-6}m$

(3) $1.4\times {10}^{-6}m$

(4) $1.1\times {10}^{-6}m$

The ratio of momenta of an electron and an $\alpha$-particle which are accelerated from rest by a potential difference of 100 volt is 

(1) 1

(2) $\sqrt{\frac{2m_e}{m_{\alpha }}}$

(3) $\sqrt{\frac{m_e}{m_{\alpha }}}$

(4) $\sqrt{\frac{m_e}{2m_{\alpha }}}$

When a proton is accelerated through 1V, then its kinetic energy will be -

(1) 1840 eV

(2) 13.6 eV

(3) 1 eV

(4) 0.54 eV

The displacement of a charge Q in the electric field $E=e_1\hat{i}+e_2\hat{j}+e_3\hat{k}$ is $\hat{r}=a\hat{i}+b\hat{j}$. The work done is 

(1) $Q(a{e}_1+b{e}_2)$

(2) $Q\sqrt{{\left(a{e}_1\right)}^2+{\left(b{e}_2\right)}^2}$

(3) $Q(e_1+e_2)\sqrt{a^2+b^2}$

(4) $Q\left(\sqrt{e_1^2+e_2^2)}\right(a+b)$

Three charges Q, +q and +q are placed at the vertices of a right-angled isosceles triangle as shown. The net electrostatic energy of the configuration is zero if Q is equal to

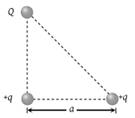
(1) $\frac{-q}{1+\sqrt{2}}$

(2) $\frac{-2q}{2+\sqrt{2}}$

(3) –2q

(4) +q