Select Question Set:
An elastic ball is projected vertically upward with a speed \(u,\) and it returns to the ground and rebounds, the motion is periodic with a period \(T.\) A simple pendulum, having a length equal to maximum altitude attained by this ball, would have a time period of:
1.
\(T\)
2.
\(\pi T\)
3.
\(\pi\sqrt2T\)
4.
\(\dfrac{\pi}{\sqrt 2}T\)
Subtopic: Angular SHM |
53%
Level 3: 35%-60%
Hints
A block \(A\) is placed on a spring and causes it to be compressed; when another block \(B\) is placed on top of the first one the compression increases by \(125\%.\) The time period of small oscillations is \(T_A\) when \(A\) is present, and is \(T_{AB},\) when both \(A~\&~B\) are present. Then,


| 1. | \(T_{AB}=\dfrac{3}{2}~T_A\) | 2. | \(T_{AB}=\dfrac{\sqrt5}{2}~T_A\) |
| 3. | \(T_{AB}=\dfrac{1}{2}~T_A\) | 4. | \(T_{AB}=\dfrac{2}{3}~T_A\) |
Subtopic: Spring mass system |
57%
Level 3: 35%-60%
Hints
A light rod \(AB\) is hinged at \(A\) so that it is free to rotate about \(A.\) It is initially horizontal with a small block of mass \(m\) attached at \(B,\) and a spring (constant - \(k\)) holding it vertically up at its mid-point. The time period of vertical oscillations of the system is:


| 1. | \(2 \pi \sqrt{\dfrac{m}{k}} \) | 2. | \(\pi \sqrt{\dfrac{m}{k}} \) |
| 3. | \(4\pi \sqrt{\dfrac{m}{k}}\) | 4. | \(\dfrac{\pi}{2} \sqrt{\dfrac{m}{k}}\) |
Subtopic: Spring mass system |
Level 4: Below 35%
Hints
Unlock IMPORTANT QUESTION
This question was bookmarked by 5 NEET 2025 toppers during their NEETprep journey. Get Target Batch to see this question.
✨ Perfect for quick revision & accuracy boost
Buy Target Batch
Access all premium questions instantly
A particle moves in a plane such that its displacements are the sum of two displacements \(\vec{ r}_1\), and \(\vec{r}_2;\) each of which undergo SHM in opposite phase with respect to the other, but of unequal amplitude. The resultant motion of the particle is:
| 1. | uniform circular motion |
| 2. | elliptical motion |
| 3. | linear SHM |
| 4. | angular SHM along a circle |
Subtopic: Simple Harmonic Motion |
Level 3: 35%-60%
Hints
A block of mass \(m\) is pushed towards a spring of spring constant \(k,\) with a speed \(u.\) It is very close to the spring, initially. After a time \(t,\) the block rebounds and returns to its initial position. If \(u\) is increased, then:


| 1. | \(t\) increases. |
| 2. | \(t\) decreases. |
| 3. | \(t\) remains unchanged. |
| 4. | the effect on \(t\) cannot be determined due to insufficient information. |
Subtopic: Spring mass system |
58%
Level 3: 35%-60%
Hints
Two springs are joined end-to-end and connected to a block of mass \(m.\) The angular frequency \((\omega)\) of oscillation is:
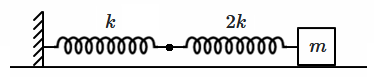

| 1. | \(\sqrt{\dfrac{2k}{3m}}\) | 2. | \(\sqrt{\dfrac{3k}{2m}}\) |
| 3. | \(\sqrt{\dfrac{3k}{m}}\) | 4. | \(\sqrt{\dfrac{k}{3m}}\) |
Subtopic: Spring mass system |
71%
Level 2: 60%+
Hints
Unlock IMPORTANT QUESTION
This question was bookmarked by 5 NEET 2025 toppers during their NEETprep journey. Get Target Batch to see this question.
✨ Perfect for quick revision & accuracy boost
Buy Target Batch
Access all premium questions instantly
Two identical simple pendulums are compared, one \((A)\) located on the surface of the earth and the other \((B)\) – at a height \((h)\) above the earth's surface: \(h=\dfrac{R}{1000}.\)
Their time periods are related as:
1. \(T_A\Big(1+\dfrac{1}{1000}\Big)=T_B\)
2. \(T_B\Big(1+\dfrac{1}{1000}\Big)=T_A\)
3. \(T_A\Big(1+\dfrac{1}{2000}\Big)=T_B\)
4. \(T_B\Big(1+\dfrac{1}{2000}\Big)=T_A\)
Their time periods are related as:
1. \(T_A\Big(1+\dfrac{1}{1000}\Big)=T_B\)
2. \(T_B\Big(1+\dfrac{1}{1000}\Big)=T_A\)
3. \(T_A\Big(1+\dfrac{1}{2000}\Big)=T_B\)
4. \(T_B\Big(1+\dfrac{1}{2000}\Big)=T_A\)
Subtopic: Angular SHM |
60%
Level 2: 60%+
Hints
Unlock IMPORTANT QUESTION
This question was bookmarked by 5 NEET 2025 toppers during their NEETprep journey. Get Target Batch to see this question.
✨ Perfect for quick revision & accuracy boost
Buy Target Batch
Access all premium questions instantly
A particle undergoes SHM with an amplitude of \(10\) cm and a time period of \(4\) s. The average velocity of the particle during the course of its motion from its mean position to its extreme position is:
1. \(5\) cm/s
2. \(10\) cm/s
3. at least \(10\) cm/s
4. at most \(10\) cm/s
1. \(5\) cm/s
2. \(10\) cm/s
3. at least \(10\) cm/s
4. at most \(10\) cm/s
Subtopic: Simple Harmonic Motion |
Level 3: 35%-60%
Hints
Unlock IMPORTANT QUESTION
This question was bookmarked by 5 NEET 2025 toppers during their NEETprep journey. Get Target Batch to see this question.
✨ Perfect for quick revision & accuracy boost
Buy Target Batch
Access all premium questions instantly
Two SHMs of the form:
\(x=A+A\text{sin}\omega t\\ y=A-A\text{sin}\omega t\)
are superposed on a particle, along \(x\) and \(y\) directions. The resultant of these motions is:
\(x=A+A\text{sin}\omega t\\ y=A-A\text{sin}\omega t\)
are superposed on a particle, along \(x\) and \(y\) directions. The resultant of these motions is:
| 1. | circular motion |
| 2. | SHM along \(x\)-axis |
| 3. | SHM along \(y\)-axis |
| 4. | SHM, but along a direction other than \(x\) or \(y\)-axis |
Subtopic: Simple Harmonic Motion |
54%
Level 3: 35%-60%
Hints
Unlock IMPORTANT QUESTION
This question was bookmarked by 5 NEET 2025 toppers during their NEETprep journey. Get Target Batch to see this question.
✨ Perfect for quick revision & accuracy boost
Buy Target Batch
Access all premium questions instantly
Given below are two statements:
| Statement I: | If the acceleration of a particle is directed towards a fixed point, and proportional to the distance from that point – the motion is SHM. |
| Statement II: | During SHM, the kinetic energy of the particle oscillates at twice the frequency of the SHM. |
| 1. | Statement I is incorrect and Statement II is correct. |
| 2. | Both Statement I and Statement II are correct. |
| 3. | Both Statement I and Statement II are incorrect. |
| 4. | Statement I is correct and Statement II is incorrect. |
Subtopic: Energy of SHM |
Level 3: 35%-60%
Hints
Select Question Set:






