If the vertical spring-mass system is dipped in a non-viscous liquid, then:
1.
Only the mean position changes.
2.
Only the time period changes.
3.
Both the time period and mean position change.
4.
Both the time period and mean position remain the same.
The displacement \( x\) of a particle varies with time \(t\) as \(x = A sin\left (\frac{2\pi t}{T} +\frac{\pi}{3} \right)\). The time taken by the particle to reach from \(x = \frac{A}{2} \) to \(x = -\frac{A}{2} \) will be:
| 1. | \(\frac{T}{2}\) | 2. | \(\frac{T}{3}\) |
| 3. | \(\frac{T}{12}\) | 4. | \(\frac{T}{6}\) |
Force on a particle \(F\) varies with time \(t\) as shown in the given graph. The displacement \(x\) vs time \(t\) graph corresponding to the force-time graph will be:
| 1. |  |
2. |  |
| 3. |  |
4. |  |
The time period of a simple pendulum in a stationary trolley is \(T_1.\) If the trolley is moving with a constant speed, then the time period is \(T_2.\) Then:
1. \(T_1>T _2\)
2. \(T_1<T _2\)
3. \(T_1=T _2\)
4. \(T_2= \infty \)
1. \(5~\text{Hz}\)
2. \(20~\text{Hz}\)
3. \(10~\text{Hz}\)
4. \(40~\text{Hz}\)
A particle is moving along the x-axis. The speed of particle v varies with position x as . The time period of S.H.M is
1.
2.
3.
4.
A block of mass \(m\) is attached to a massless spring of spring constant \(k,\) with the other end of the spring fixed to the wall of a trolley. Initially, the spring is unstretched, and the trolley begins to move rightward with a velocity that increases linearly with time, as shown in the velocity-time \((v\text-t)\) graph.
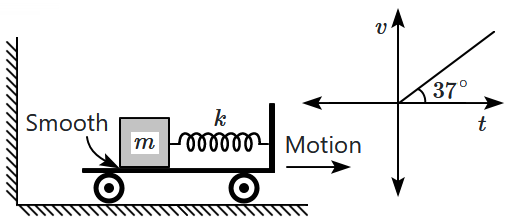
The total energy of oscillation of the block as observed from the trolley frame is:
| 1. | \(\dfrac{32m^2}{6k}\) | 2. | \(\dfrac{9m^2}{8k}\) |
| 3. | \(\dfrac{9m^2}{32k}\) | 4. | \(\dfrac{8m^2}{9k}\) |
A body of mass \(20\) g is executing SHM with amplitude \(5\) cm. When it passes through the equilibrium position its speed is \(20\) cm/s. What would be the distance from equilibrium when its speed becomes \(10\) cm/s?
1. \(\frac{5\sqrt{3}}{4}\) cm
2. \(\frac{5\sqrt{3}}{2}\) cm
3. \(\frac{25\sqrt{7}}{2}\) cm
4. \(5\sqrt{3}\) cm
For a simple harmonic oscillator, a velocity-time diagram is shown. The angular frequency of oscillation is:
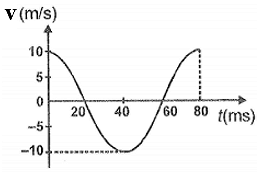
1. rad/s
2. rad/s
3. 25 rad/s
4. 25 rad/s
In an S.H.M, when the displacement is one-fourth of the amplitude, the ratio of total energy to the potential energy is
1. 16: 1
2. 1: 16
3. 1: 8
4. 8: 1







