The coefficient of area expansion \(\beta\) of a rectangular sheet of a solid in terms of the coefficient of linear expansion \(\alpha\) is:
1. \(2\alpha\)
2. \(\alpha\)
3. \(3\alpha\)
4. \(\alpha^2\)
A blacksmith fixes an iron ring on the rim of the wooden wheel of a horse cart. The diameter of the rim and the iron ring are \(5.012\) m and \(5.00\) m, respectively at \(27^{\circ}\text{C}.\) To what temperature should the ring be heated so as to fit the rim of the wheel?
\(\left(\text{Given:}~\alpha~\text{for iron}= 1.20 \times 10^{-5}~^\circ{\text{C}^{-1}}\right)\)
1. \(128^{\circ}\text{C}\)
2. \(118^{\circ}\text{C}\)
3. \(227^{\circ}\text{C}\)
4. \(218^{\circ}\text{C}\)
A sphere of \(0.047\) kg aluminium is placed for sufficient time in a vessel containing boiling water so that the sphere is at \(100^{\circ}\text{C}\). It is then immediately transferred to a \(0.14\) kg copper calorimeter containing \(0.25\) kg water at \(20^{\circ}\text{C}\). The temperature of water rises and attains a steady-state at \(23^{\circ}\text{C}\). The specific heat capacity of aluminium is:
(Given that: Specific heat capacity of copper calorimeter \(= 0.386\times 10^{3}~\text{J kg}^{-1}\text{K}^{-1}\) and the specific heat capacity of water \(s_w= 4.18\times 10^{3}~\text{J kg}^{-1}\text{K}^{-1})\)
1. \(1.811~\text{kJ kg}^{-1}\text{K}^{-1}\)
2. \(1.911~\text{kJ kg}^{-1}\text{K}^{-1}\)
3. \(0.811~\text{kJ kg}^{-1}\text{K}^{-1}\)
4. \(0.911~\text{kJ kg}^{-1}\text{K}^{-1}\)
When \(0.15\) kg of ice at \(0^\circ \text{C}\) is mixed with \(0.30\) kg of water at \(50^\circ \text{C}\) in a container, the resulting temperature is \(6.7^\circ \text{C}.\)
The heat of fusion of ice is: (\(S_{\text{water}}=4186\) J kg–1 K–1)
1. \( 3.43 \times 10^4\) Jkg–1
2. \( 3.34 \times 10^4\) Jkg–1
3. \( 3.34 \times 10^5\) Jkg–1
4. \(4.34 \times 10^5\) Jkg–1
(given, the specific heat capacity of \(\text{ice}= 2100~\text{J kg}^{-1}\text{K}^{-1},\) the specific heat capacity of \(\text{water}= 4186~\text{J kg}^{-1}\text{K}^{-1},\) the latent heat of fusion of \(\text{ice}= 3.35\times 10^{5}~\text{J kg}^{-1}\) and the latent heat of \(\text{steam}= 2.256\times 10^6~\text{J kg}^{-1}\))
| 1. | \(9.1\times 10^{7}~\text{J}\) | 2. | \(8.1\times 10^{6}~\text{J}\) |
| 3. | \(9.1\times 10^{6}~\text{J}\) | 4. | \(8.1\times 10^{7}~\text{J}\) |
What is the temperature of the steel-copper junction in the steady-state of the system shown in the figure? The length of the steel rod = \(15.0\) cm, length of the copper rod = \(10.0\) cm, temperature of the furnace = \(300^{\circ}\text{C}\), temperature of the other end = \(0^{\circ}\text{C}\). The area of the cross section of the steel rod is twice that of the copper rod. (Thermal conductivity of steel = \(50.2 ~\text{J s}^{-1}\text{m}^{-1}\text{K}^{-1};\) and of copper \(= 385~\text{J s}^{-1}\text{m}^{-1}\text{K}^{-1})\).
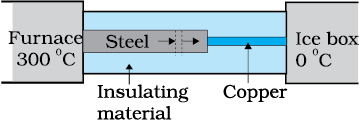
1. \(44.4^{\circ}\text{C}\)
2. \(44.4~\text{K}\)
3. \(54.4^{\circ}\text{C}\)
4. \(54.4~\text{K}\)
An iron bar
\(\left(L_{1}=0.1 \text{m} , A_{1}=0.02~\text{m}^{2} , K_{1}=79~\text{Wm}^{- 1} \text{K}^{-1}\right)\) and a brass bar
\(\left(L_{2}=0.1~\text{m} , A_{2}=0.02~\text{m}^{2} , K_{2}=109~\text{Wm}^{- 1} \text{K}^{- 1}\right)\) are soldered end to end as shown in the figure. The free ends of the iron bar and brass bar are maintained at \(373~ \text{K}\) and \(273~ \text{K}\) respectively. The temperature of the junction of the two bars is:

1. \(215~ \text{K}\)
2. \(315~ \text{K}\)
3. \(415~ \text{K}\)
4. \(115~ \text{K}\)
1. \(50\) s
2. \(52\) s
3. \(42\) s
4. \(48\) s
An iron bar \(K_1 = 79~\text{W m}^{-1}\text{K}^{-1}\) and a brass bar \(K_2 = 109~\text{W m}^{-1}\text{K}^{-1}\) are soldered end to end as shown in the figure. The free ends of the iron bar and brass bar are maintained at \(373\) K and \(273\) K respectively. Then the equivalent thermal conductivity of the compound bar is:

| 1. | \(94.6~\text{W m}^{-1}\text{K}^{-1}\) | 2. | \(93.6~\text{W m}^{-1}\text{K}^{-1}\) |
| 3. | \(81.6~\text{W m}^{-1}\text{K}^{-1}\) | 4. | \(91.6~\text{W m}^{-1}\text{K}^{-1}\) |
An iron bar \(\left(L_{1} = 0 . 1 ~ \text{m}, A_{1} = 0 . 02 ~\text{m}^{2}, K_{1} = 79~\text{W m}^{- 1} \text{K}^{- 1}\right)\) and a brass bar \(\left(L_{2}= 0 . 1 ~\text{m}, A_2 = 0.02~\text{m}^2, K_2 = 109~\text{W m}^{-1}\text{K}^{-1}\right)\) are soldered end to end as shown in the figure. The free ends of the iron bar and brass bar are maintained at \(373\) K and \(273\) K respectively. The heat current through the compound bar is:

1. \(916.1\) W
2. \(826.1\) W
3. \(926.1\) W
4. \(726\) W






