The value of the coefficient of volume expansion of glycerine is \(5\times10^{-4}~\text{K}^{-1}.\) The fractional change in the density of glycerine for a rise of \(40^\circ \text{C}\) in its temperature is:
| 1. | \(0.015\) | 2. | \(0.020\) |
| 3. | \(0.025\) | 4. | \(0.010\) |
On observing light from three different stars \(P,\) \(Q,\) and \(R,\) it was found that the intensity of the violet colour is maximum in the spectrum of \(P,\) the intensity of the green colour is maximum in the spectrum of \(R\) and the intensity of the red colour is maximum in the spectrum of \(Q.\) If \(T_P,\) \(T_Q,\) and \(T_R\) are the respective absolute temperatures of \(P,\) \(Q,\) and \(R,\) then it can be concluded from the above observations that:
1. \(T_P>T_Q>T_R\)
2. \(T_P>T_R>T_Q\)
3. \(T_P<T_R<T_Q\)
4. \(T_P<T_Q<T_R\)
The two ends of a metal rod are maintained at temperatures \(100~^\circ\text{C}\) and \(110~^\circ\text{C}.\) The rate of heat flow in the rod is found to be \(4.0\) J/s. If the ends are maintained at temperatures \(200~^\circ \text{C}\) and \(210 ~^\circ \text{C},\) the rate of heat flow will be:
1. \(44.0\) J/s
2. \(16.8\) J/s
3. \(8.0\) J/s
4. \(4.0\) J/s
Steam at \(100~^{\circ}\text{C}\) is passed into \(20~\text{g}\) of water at \(10~^{\circ}\text{C}.\) When water acquires a temperature of \(80~^{\circ}\text{C},\) the mass of water present will be:
[Take specific heat of water \(= 1~\text{cal g}^{-1}~^\circ\text{C}^{-1}\) and latent heat of steam \(= 540~\text{cal g}^{-1}\)]
1. \(24~\text{g}\)
2. \(31.5~\text{g}\)
3. \(42.5~\text{g}\)
4. \(22.5~\text{g}\)
A certain quantity of water cools from \(70~^{\circ}\text{C}\) to \(60~^{\circ}\text{C}\) in the first \(5\) minutes and to \(54~^{\circ}\text{C}\) in the next \(5\) minutes. The temperature of the surroundings is:
1. \(45~^{\circ}\text{C}\)
2. \(20~^{\circ}\text{C}\)
3. \(42~^{\circ}\text{C}\)
4. \(10~^{\circ}\text{C}\)
| 1. | Wien’s displacement Law |
| 2. | Kirchhoff’s Law |
| 3. | Newton’s Law of cooling |
| 4. | Stefan’s Law |
| 1. | \(K_1 A_1=4K_2 {A}_2 \) | 2. | \(K_1 {A}_1=2 {K}_2 {A}_2 \) |
| 3. | \(4 {K}_1{A}_1={K}_2 {A}_2 \) | 4. | \({K}_1 {A}_1={K}_2 {A}_2\) |
1. \(3 \times 10^{-4} / ^\circ\text C\)
2. \(2 \times 10^{-4} / ^\circ\text C\)
3. \(6 \times 10^{-4} / ^\circ\text C\)
4. \(10^{-4} / ^\circ\text C\)
If the radius of a star is \(R\) and it acts as a black body, what would be the temperature of the star at which the rate of energy production is \(Q?\)
\(\left(\sigma~ \text{is Stefan-Boltzmann constant}\right)\)
1. \(\dfrac{Q}{4\pi R^2\sigma}\)
2. \(\left(\dfrac{Q}{4\pi R^2\sigma}\right )^{\dfrac{-1}{2}}\)
3. \(\left(\dfrac{4\pi R^2 Q}{\sigma}\right )^{\dfrac{1}{4}}\)
4. \(\left(\dfrac{Q}{4\pi R^2 \sigma}\right)^{\dfrac{1}{4}}\)
Liquid oxygen at \(50~\text K\) is heated up to \(300~\text K\) at a constant pressure of \(1~\text{atm}.\) The rate of heating is constant. Which one of the following graphs represents the variation of temperature with time?
| 1. |  |
2. | 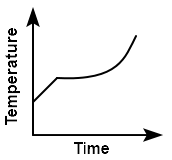 |
| 3. |  |
4. |  |






