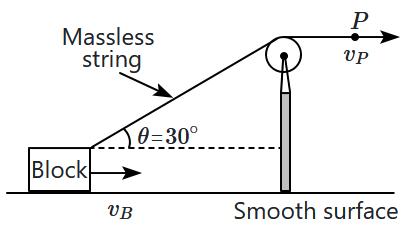
What is the velocity of the block when the angle between the string and horizontal is \(30^\circ\) as shown in the diagram?

          
1. \(v_B=v_P\)
2. \(v_B=\frac{v_P}{\sqrt{3}}\)
3. \(v_B=2v_P\)
4. \(v_B=\frac{2v_P}{\sqrt{3}}\)

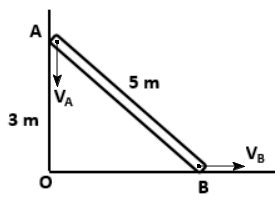
The figure shows a rod of length \(5\) m. Its ends, \(A\) and \(B\), are restrained to moving in horizontal and vertical guides. When the end \(A\) is \(3\) m above \(O\), it moves at \(4\) m/s. The velocity of end \(B\) at that instant is:
         
1. \(2\) m/s
2. \(3\) m/s
3. \(4\) m/s
4. \(0.20\) m/s

If the block is being pulled by the rope moving at speed \(v\) as shown, then the horizontal velocity of the block is:

                           
1. \(v\)
2. \(v\cos\theta\)
3. \(\frac{v}{\cos\theta}\)
4. \(\frac{v}{\sin\theta}\)

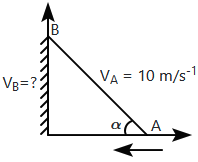
A rigid rod is placed against the wall as shown in the figure. When the velocity at its lower end is \(10\) ms^-1 and its base makes an angle \(\alpha=60^\circ\) with horizontal, then the vertical velocity of its end \(\mathrm{B}\) (in ms^-1) will be: