A solid sphere of mass \(M\) and the radius \(R\) is in pure rolling with angular speed \(\omega\) on a horizontal plane as shown in the figure. The magnitude of the angular momentum of the sphere about the origin \(O\) is:
                     

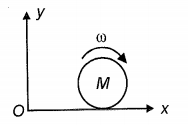
1. \(\frac{7}{5} M R^{2} \omega\)
2. \(\frac{3}{2} M R^{2} \omega\)
3. \(\frac{1}{2} M R^{2} \omega\)
4. \(\frac{2}{3} M R^{2} \omega\)$$

A thin circular ring of mass \(M\) and radius \(R\) is rotating about its axis with a constant angular velocity \(\omega\)$$.  Four objects of mass \(m\) are held gently at the opposite ends of the ring's two perpendicular diameters. The angular velocity of the ring will be:
1. \(\dfrac{M\omega}{M+4m}\)
2. \(\dfrac{(M+4m)\omega}{M}\)
3. \(\dfrac{(M-4m)\omega}{M+4m}\)
4. \(\dfrac{M\omega}{4m}\)

A boy is standing on a disc rotating about the vertical axis passing through its centre. He pulls his arms towards himself, reducing his moment of inertia by a factor of m. The new angular speed of the disc becomes double its initial value. If the moment of inertia of the boy is I₀ , then the moment of inertia of the disc will be:

1.  $2{\mathrm{I}}_{0}m$

2.  ${\mathrm{I}}_0\left(1-\frac{2}{m}\right)$

3.  ${\mathrm{I}}_0\left(1-\frac{1}{m}\right)$

4.  $\left(\frac{{\mathrm{I}}_0}{2m}\right)$

A rod is falling down with constant velocity \(V_0\) as shown. It makes contact with hinge A and rotates around it. The angular velocity of the rod just after the moment when it comes in contact with hinge A is:

The law of conservation of angular momentum is valid when:

The position of a particle is given by \(\vec r = \hat i+2\hat j-\hat k\) and momentum \(\vec P = (3 \hat i + 4\hat j - 2\hat k)\). The angular momentum is perpendicular to:

A particle of mass \(m\) moves in the\(XY\) plane with a velocity of \(v\) along the straight line \(AB.\) If the angular momentum of the particle about the origin \(O\) is \(L_A\) when it is at \(A\) and \(L_B\) when it is at \(B,\) then: