The moment of inertia of a uniform circular disc of radius 'R' and mass 'M' about an axis touching the disc at its diameter and normal to the disc will be:
1. $\frac{3}{2}M{R}^2$
2. $\frac{1}{2}M{R}^2$
3. $M{R}^2$
4. $\frac{2}{5}M{R}^2$

The moment of inertia of a uniform circular disc is maximum about an axis perpendicular to the disc and passing through:
 
1. B                   
2. C
3. D                   
4. A

In the three figures, each wire has a mass M, radius R and a uniform mass distribution. If they form part of a circle of radius R, then about an axis perpendicular to the plane and passing through the centre (shown by crosses), their moment of inertia is in the order:

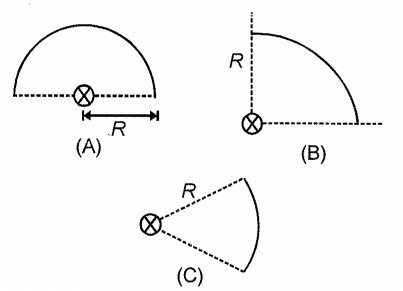
1.  $I_A$ $>$ $I_B$ $>$ $$ $I_C$

2.  $I_A$ $=$ $I_B$ $=$ $I_C$

3.  $I_A$ $<$ $I_B$ $<$ $I_C$

4.  $I_A$ $<$ $I_C$ $<$ $I_B$

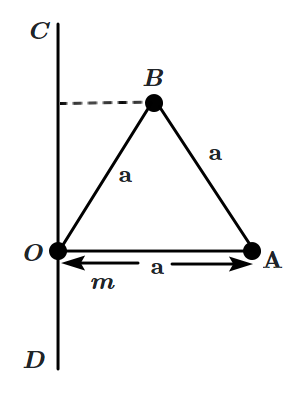
Three-point masses each of mass \(m,\) are placed at the vertices of an equilateral triangle of side \(a.\) The moment of inertia of the system through a mass \(m\) at \(O\) and lying in the plane of \(COA\) and perpendicular to \(OA\) is:

Four masses are joined to light circular frames as shown in the figure. The radius of gyration of this system about an axis passing through the center of the circular frame and perpendicular to its plane would be: (where 'a' is the radius of the circle)
                   
1.  $\frac{a}{\sqrt{2}}$

2.  $\frac{a}{2}$

3.  a

4.  2a

               
1. \(\frac{5}{3}mL^2\)
2. \(4mL^2\)
3. \(\frac{1}{4}mL^2\)
4. \(\frac{2}{3}mL^2\)