If a body is moving in a circular path with decreasing speed, then: (symbols have their usual meanings):

1.  $\overrightarrow{r}.\overrightarrow{\omega }$ $=$ $$ $0$

2.  $\overrightarrow{\tau }.\overrightarrow{v}$ $=$ $0$

3.  $\overrightarrow{a}.\overrightarrow{v}$ $<$ $0$

4.  All of these

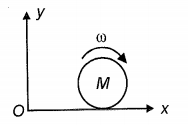
A solid sphere of mass \(M\) and radius \(R\) is in pure rolling with angular speed $\omega$ on a horizontal plane as shown. The magnitude of the angular momentum of the sphere about the origin \(O\) is:
             

1.  $\frac{7}{5}M{R}^2\omega$

2.  $\frac{3}{2}M{R}^2\omega$

3.  $\frac{1}{2}M{R}^2\omega$

4.  $\frac{2}{3}M{R}^2\omega$

A boy is standing on a disc rotating about the vertical axis passing through its centre. He pulls his arms towards himself, reducing his moment of inertia by a factor of m. The new angular speed of the disc becomes double its initial value. If the moment of inertia of the boy is I₀ , then the moment of inertia of the disc will be:

1.  $2{\mathrm{I}}_{0}m$

2.  ${\mathrm{I}}_0\left(1-\frac{2}{m}\right)$

3.  ${\mathrm{I}}_0\left(1-\frac{1}{m}\right)$

4.  $\left(\frac{{\mathrm{I}}_0}{2m}\right)$

Four masses are joined to light circular frames as shown in the figure. The radius of gyration of this system about an axis passing through the center of the circular frame and perpendicular to its plane would be: (where 'a' is the radius of the circle)
                   
1.  $\frac{a}{\sqrt{2}}$

2.  $\frac{a}{2}$

3.  a

4.  2a

               
1. \(\frac{5}{3}mL^2\)
2. \(4mL^2\)
3. \(\frac{1}{4}mL^2\)
4. \(\frac{2}{3}mL^2\)

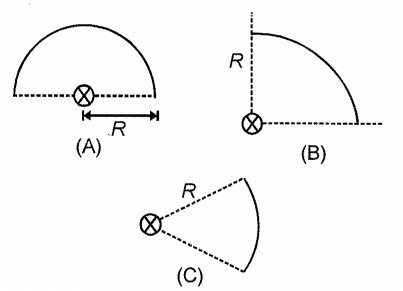
In the three figures, each wire has a mass M, radius R and a uniform mass distribution. If they form part of a circle of radius R, then about an axis perpendicular to the plane and passing through the centre (shown by crosses), their moment of inertia is in the order:

1.  $I_A$ $>$ $I_B$ $>$ $$ $I_C$

2.  $I_A$ $=$ $I_B$ $=$ $I_C$

3.  $I_A$ $<$ $I_B$ $<$ $I_C$

4.  $I_A$ $<$ $I_C$ $<$ $I_B$

The value of \(M\), as shown, for which the rod will be in equilibrium is:
      

Particles \(A\) and \(B\) are separated by \(10\) m, as shown in the figure. If \(A\) is at rest and \(B\) started moving with a speed of \(20\) m/s then the angular velocity of \(B\) with respect to \(A\) at that instant is:

The law of conservation of angular momentum is valid when: