If a particle moves in a circle with a constant angular speed \((\omega)\) about point \(O\), then its angular speed about point \(A\) will be:
           
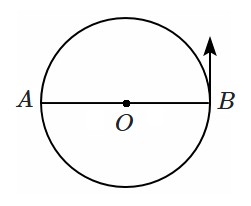
1. \(2\omega\)
2. \(\frac{\omega}{2}\)
3. \(\omega\)
4. \(\frac{\omega}{4}\)

Which of the following is the value of the torque of force \(F\) about origin \(O:\)

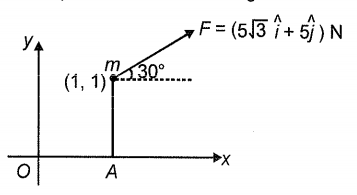
1. \(\vec{\tau}=5(1-\sqrt{3}) \hat{k}\) N-m
2. \(\vec{\tau}=5(1-\sqrt{3}) \hat{j}\) N-m
3. \(\vec{\tau}=5(\sqrt{3}-1) \hat{i}\) N-m
4. \(\vec{\tau}=\sqrt{3} \hat{j}\) N-m

Four thin rods, each of mass m and length L, form a square. The moment of inertia on any side of the square is:

             
1.  $\frac{5}{3}m{L}^2$

2.  $4$ $m{l}^2$

3.  $\frac{m{L}^2}{4}$

4.   $\frac{2}{3}m{L}^2$

In the three figures, each wire has a mass M, radius R and a uniform mass distribution. If they form part of a circle of radius R, then about an axis perpendicular to the plane and passing through the centre (shown by crosses), their moment of inertia is in the order:

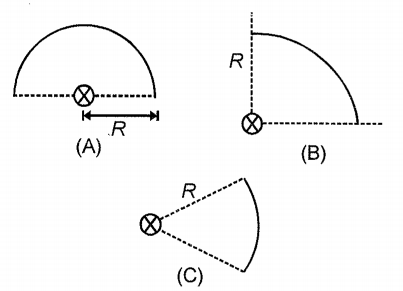
1.  $I_A$ $>$ $I_B$ $>$ $$ $I_C$

2.  $I_A$ $=$ $I_B$ $=$ $I_C$

3.  $I_A$ $<$ $I_B$ $<$ $I_C$

4.  $I_A$ $<$ $I_C$ $<$ $I_B$

The value of \(M\), as shown, for which the rod will be in equilibrium is:
      

Particles \(A\) and \(B\) are separated by \(10\) m, as shown in the figure. If \(A\) is at rest and \(B\) started moving with a speed of \(20\) m/s then the angular velocity of \(B\) with respect to \(A\) at that instant is:

A uniform cubical block of side L rests on a rough horizontal surface with coefficient of friction $\mu$. A horizontal force F is applied on the block as shown. If there is sufficient friction between the block and the ground, then the torque due to normal reaction about its centre of mass is:

1.  $Zero$

2.  $FL$

3.  $\frac{FL}{2}$

4.  $\frac{3FL}{2}$

A bomb is projected from the ground at a horizontal range of \(R\). If the bomb explodes mid-air, then the range of its centre of mass is:
1. \(\frac{R}{2}\)
2. \(R\)
3. \(2R\)
4. \(\frac{2R}{3}\)