1. \(5\) m
2. \(3\) m
3. \(1\) m
4. \(4\) m
The ratio of the radius of gyration of a circular disc to that of a circular ring, both having the same mass and radius, about their respective axes is:
| 1. | \(\sqrt2:\sqrt3\) | 2. | \(\sqrt3:\sqrt2\) |
| 3. | \(1:\sqrt2\) | 4. | \(\sqrt2:1\) |
Five particles of mass \(2\) kg each are attached to the circumference of a circular disc of a radius of \(0.1\) m and negligible mass. The moment of inertia of the system about the axis passing through the centre of the disc and perpendicular to its plane will be:
1. \(1\) kg-m2
2. \(0.1\) kg-m2
3. \(2\) kg-m2
4. \(0.2\) kg-m2
1. \(\frac14MR^2\)
2. \(\frac12MR^2\)
3. \(MR^2\)
4. \(\frac32MR^2\)
The ratio of the moments of inertia of two spheres, about their diameters, having the same mass and their radii being in the ratio of \(1:2\), is:
| 1. | \(2:1\) | 2. | \(4:1\) |
| 3. | \(1:2\) | 4. | \(1:4\) |
The moment of inertia of a thin uniform circular disc about one of its diameter is I. Its moment of inertia about an axis perpendicular to the circular surface and passing through its center will be:
1.
2. 2 l
3.
4.
1. \(\frac{m_1m_2}{m_1+m_2}l^2\)
2. \(\frac{m_1+m_2}{m_1m_2}l^2\)
3. \((m_1+m_2)l^2\)
4. \(\sqrt{(m_1m_2)}l^2\)
In the three figures, each wire has a mass M, radius R and a uniform mass distribution. If they form part of a circle of radius R, then about an axis perpendicular to the plane and passing through the centre (shown by crosses), their moment of inertia is in the order:
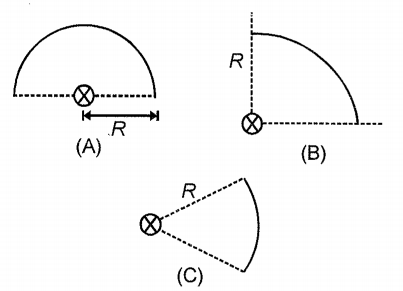
1.
2.
3.
4.
The one-quarter sector is cut from a uniform circular disc of radius \(R\). This sector has a mass \(M\). It is made to rotate about a line perpendicular to its plane and passing through the centre of the original disc. Its moment of inertia about the axis of rotation will be:

| 1. | \(\frac{1}{2} M R^2 \) | 2. | \(\frac{1}{4} M R^2 \) |
| 3. | \(\frac{1}{8} M R^2 \) | 4. | \(\sqrt{2} M R^2\) |
A circular disc is to be made by using iron and aluminium so that it acquires a maximum moment of inertia about its geometrical axis. It is possible with:
| 1. | Aluminium in the interior and iron surrounding it |
| 2. | Iron at the interior and aluminium surrounding it |
| 3. | Using iron and aluminium layers in alternate order |
| 4. | A sheet of iron is used at both the external surface and aluminium sheet as the internal layer |






