Ncert Exercises & Solutions

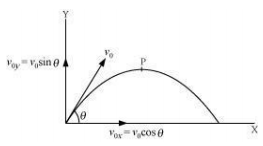
4.32 (a) Show that for a projectile the angle between the velocity and the x-axis as a function of time is given by

$θ (t) = \tan^{- 1} (\frac{v_{0 y} - g t}{v_{0 x}})$

(b) Shows that the projection angle θ₀for a projectile launched from the origin is given by

$θ_{0} = \tan^{- 1} (\frac{4 h_{e n}}{R})$

where the symbols have their usual meaning.

NEETprep Answer:

Let

v_{0 x} and v_{0 y}

respectively be the initial components of the velocity of the projectile along horizontal (x) and vertical (y) directions.

Let

v_{x} and v_{y}

respectively be the horizontal and vertical components of velocity at a point P.

Time is taken by the projectile to reach point P = t
Applying the first equation of motion along with the vertical and horizontal directions, we get:

\begin{array}{l} v_{y} = v_{0 y} = gt \\ And v_{x} = v_{0 x} \\ ∴ \tan θ = \frac{v_{y}}{v_{x}} = \frac{v_{0 y} - gt}{v_{0 x}} \\ θ = \tan^{- 1} (\frac{v_{0 y} - gt}{v_{0 x}}) \end{array}

Maximum vertical height

h_{m} = \frac{u_{0}^{2} \sin^{2} 2 θ}{2 g} . . . (i)

Horizontal range,

R = \frac{u_{0}^{2} \sin^{2} 2 θ}{g} . . . (ii)

Solving equations (i) and (ii), we get:

\begin{array}{l} - \frac{h_{m}}{R} = \frac{\sin^{2} θ}{2 \sin^{2} θ} \\ = \frac{\sin θ \times \sin θ}{2 \times 2 \sin θcos θ} \\ = \frac{1}{4} \frac{\sin θ}{\cos θ} = \frac{1}{4} \tan θ \\ \tan θ = (\frac{4 h_{m}}{R}) \\ θ = \tan^{- 1} (\frac{4 h_{m}}{R}) \end{array}