(a) Step 1: Find the angle subtended by the diameter of the earth.

The angle subtended at distance r due to an arc of length l is:

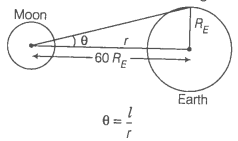
Given,

$\mathrm{l}={\mathrm{R}}_{\mathrm{E}}; \mathrm{r}=60{\mathrm{R}}_{\mathrm{E}}$
$\mathrm{\theta }=\frac{{\mathrm{R}}_{\mathrm{E}}}{60{\mathrm{R}}_{\mathrm{E}}}=\frac{1}{60}\mathrm{rad}=\frac{1}{60}\times \frac{180}{\mathrm{\pi }}\text{ degree }=\frac{3}{\mathrm{\pi }}=1^{\circ }$

Hence. the angle subtended by the diameter of the earth $=2\mathrm{\theta }=2^{\circ }$.

(b) Step 2: Find the size of the moon as compared to the earth.

Given that moon is seen as of $\left(\frac{1}{2}\right)°$ diameter and the earth is seen as of 2° diameter.

$\text{ Hence, }\frac{\text{ Diameter of earth }}{\text{ Diameter of moon }}=\frac{(2/\mathrm{\pi })\mathrm{rad}}{\left(\frac{1}{2\mathrm{\pi }}\right)\mathrm{rad}}=4$

(c) Step 3: Find the ratio of diameters of the sun and the earth.

From parallax, measurement given that the sun is at a distance of about
400 times the earth-moon distance, hence, $\frac{{\mathrm{r}}_{\mathrm{sun}}}{{\mathrm{r}}_{\text{ moon }}}=400$
 (Suppose, where r stands for distance and D for diameter)
The sun and moon both appear to be of the same angular diameter as seen from the earth.

$\begin{array}{l}\therefore \frac{{\mathrm{D}}_{\text{ sun }}}{{\mathrm{r}}_{\text{ sun }}}=\frac{{\mathrm{D}}_{\text{ moon }}}{{\mathrm{r}}_{\text{ moon }}}\\ \therefore \frac{{\mathrm{D}}_{\text{ sun }}}{{\mathrm{D}}_{\text{ moon }}}=400\end{array}$
$\mathrm{But}$
$\begin{array}{l}\frac{{\mathrm{D}}_{\text{ earth }}}{{\mathrm{D}}_{\text{ moon }}}=4\\ \therefore \frac{{\mathrm{D}}_{\text{ sun }}}{{\mathrm{D}}_{\text{ earth }}}=100\end{array}$