Ncert Exercises & Solutions

Refer to the graph in the figure. Match the following

Graph Characteristics

(a) (i) has v > 0 and a < 0 throughout

(b) (ii) has x > 0 throughout and has a point with v = 0 and a point with a = 0

(d) (iv) has v < 0 and a > 0

Hint: slope of x-t curve = velocity, rate of change in slope = acceleration.

Step 1: We have to analyze the slope of each curve i.e.,

\frac{dx}{dt} .

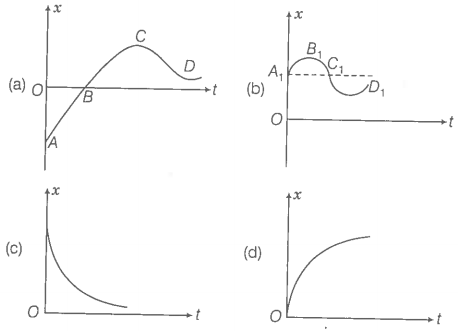
For graph (a),

Here the initial position of the particle is in the negative x-direction and at point B its position is zero.

Hence, graph (a) is matches with option (iii)

For graph (b),

x is positive for t > 0. And at point $B_{1}$ slope is zero (i.e., v = 0) and at point, acceleration is zero So, graph (b) is matched with (ii)

For graph (c),

Here slope is negative and decreasing in negative direction (i.e., v < 0 and a > 0) So, graph (c) will matches with option ().

For graph (d),

Here slope is positive and is decreasing (i.e., v > 0 and a < 0)Hence, in graph (d) will matches with option (i)

Step 2: Conclusion

Thus, we conclude that

(a) matches with (iii)

(b) matches with (ii)

And

(d) matches with (i)