For first stone:
Initial velocity, u = 15 m/s
Acceleration, a = –g = – 10 m/s2
Using the relation,
x1 = x0 + u1t + (1/2)at2
Where, height of the cliff, x0 = 200 m
x1 = 200 + 15t - 5t2 ......(i)
When this stone hits the ground, x1 = 0
– 5t2 + 15t + 200 = 0
t2 – 3t – 40 = 0
t2 – 8t + 5t – 40 = 0
t (t – 8) + 5 (t – 8) = 0
t = 8 s or t = – 5 s
Since the stone was projected at time t = 0, the negative sign before time is meaningless.
So,t = 8 s
For second stone:
Initial velocity, u = 30 m/s
Acceleration, a = – g = – 10 m/s2
Acceleration, a = – g = – 10 m/s2
Using the relation,
At the moment when this stone hits the ground; x2 = 0
t (t – 10) + 4 (t – 10) = 0
t (t – 10) (t + 4) = 0
t = 10 s or t = – 4 s
Here again, the negative sign is meaningless.
So, t = 10 s
Subtracting equations (i) and (ii), we get
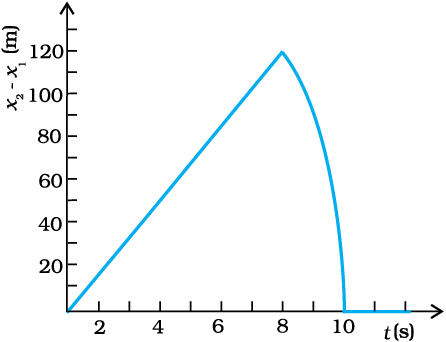
x2 - x1 =15t ....... (iii)
Equation (iii) represents the linear path of both stones. Due to this linear relation between (x2 – x1)
The maximum
separation between the two stones is at t = 8 s.
(x2 – x1)max = 15× 8 = 120 m
This is in accordance with the given graph.
After 8 s, only the second stone is in motion whose variation with time is given by the quadratic equation,
x2 – x1 = 200 + 30t – 5t2
Hence, the equation of linear and curved path is given by,
x2 – x1 = 15t (Linear path)
x2 – x1 = 200 + 30t – 5t2 (Curved path)
After 10 secs, both the stone are on the ground, so relative distance is zero and this is represented by a horizontal line after 10 secs