3.2 The position-time (x-t) graphs for two children A and B returning from their school O to their homes P and Q respectively are shown in Fig. 3.19. Choose the correct entries in the brackets below ;
(a) (A/B) lives closer to the school than (B/A)
(b) (A/B) starts from the school earlier than (B/A)
(c) (A/B) walks faster than (B/A)
(d) A and B reach home at the (same/different) time
(e) (A/B) overtakes (B/A) on the road (once/twice).
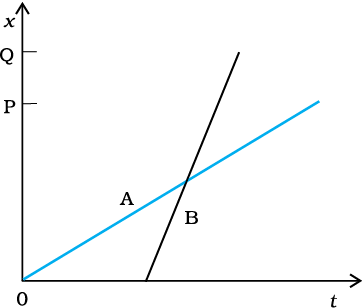
Fig. 3.19:

© 2026 GoodEd Technologies Pvt. Ltd.