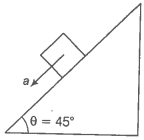
Q. 35 When a body slides down from rest along a smooth inclined plane making an angle of 45 with the horizontal, it takes time T. When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance, it is seen to take time pT, where p is some number greater than 1. Calculate the coefficient of friction between the body and the rough plane.

© 2026 GoodEd Technologies Pvt. Ltd.