Ncert Exercises & Solutions

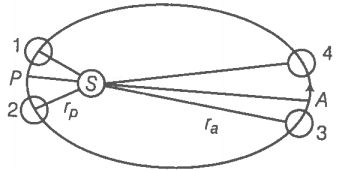
Q. 37 Earth’s orbit is an ellipse with an eccentricity of 0.0167. Thus, the earth's distance from the sun and speed as it moves around the sun varies from day-to-day. This means that the length of the solar day is not constant throughout the year. Assume that the earth's spin axis is normal to its orbital plane and find out the length of the shortest and the longest day. A day should be taken from noon to noon. Does this explain variation of length of the day during the year?

Hint: Use Kepler's laws of planetary motion.

step 1: Find the angular velocities at the apogee and perigee.

Consider the diagram. Let m be the mass of the earth,

v_{p}, v_{a}

be the velocity of the earth at perigee and apogee respectively. Similarly,

ω_{p} and ω_{a}

are corresponding angular velocities.

Angular momentum and areal velocity are constant as the earth orbits the sun.

At perigee,

r_{p}^{2} ω_{p} = r_{a}^{2} ω_{a}

at apogee ...(i)

If a is the semi-major axis of the earth's orbit, then

r_{p} = a (1 - e) a n d r_{a} = a (1 + e)

...(ii)

∴ \frac{ω_{p}}{ω_{a}} = {(\frac{1 + e}{1 - e})}^{2}, e = 0.0167

[From Eqs. (i) and (ii)]

∴ \frac{ω_{p}}{ω_{a}} = 1.0691

Let

ω

be angular speed which is the geometric mean of

ω_{p} a n d ω_{a}

and corresponds to mean solar day,

∴ (\frac{ω_{p}}{ω}) (\frac{ω}{ω_{a}}) = 1.0691

∴ \frac{ω_{p}}{ω} = \frac{ω}{ω_{a}} = 1.034

Step 2: Find if it explains the variation of the length of the day during year.

ω

corresponding to

1 °

per day (mean angular speed), then

ω_{p}

= 1.034 °

per day and

ω_{a} = 0.967 °

per day. Since, 361

°

=24 h, mean solar day, we get 361.034

°

which corresponds to 24 h, 8.14"(8.1" longer) and 360.967

°

corresponds to 23 h 59 min 52"(7.9" smaller). This does not explain the actual variation of the length of the day during the year.

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions