Ncert Exercises & Solutions

A particle is in linear simple harmonic motion between two points \(A\) and \(B,\) \(10~\text{cm}\) apart (figure.) Take the direction from \(A\) to \(B\) as the positive direction.

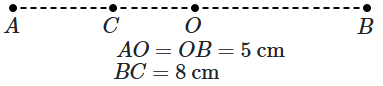
(a)	The sign of velocity, acceleration and force on the particle, when it is \(3~\text{cm}\) away from \(A\) going towards \(B,\) are positive.
(b)	The sign of velocity of the particle at \(C\) going towards \(B\) is negative.
(c)	The sign of velocity, acceleration and force on the particle, when it is \(4~\text{cm}\) away from \(B\) going towards \(A,\) are negative.
(d)	The sign of acceleration and force on the particle when it is at point \(B\) is negative.

The correct statement/s is/are:
1. (a), (b), (d)
2. (a), (c), (d)
3. (b), (c), (d)
4. (c), (d)

(2) Hint: The direction and velocity and acceleration of the particle depend on the position of the particle.

Consider the diagram.

Step 1: Find the direction and velocity and acceleration of the particle at different positions.

1. When the particle is 3 cm away from A going towards B, velocity is towards AB i.e., positive.

In SHM, acceleration is always towards the mean position (O) in this case.

Hence, it is positive.

2. When the particle is at C, velocity is towards B, hence positive.

3. When the particle is 4 cm away from B going towards A, velocity is negative and acceleration is towards mean position (O), hence, negative.

4. Acceleration is always towards mean position (O). When the particle is at B, acceleration and force are towards BA that is negative.

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions