Ncert Exercises & Solutions

14.13 Figure 14.26 (a) shows a spring of force constant k clamped rigidly at one end and a mass m attached to its free end. A force F applied at the free end stretches the spring. Figure 14.26 (b) shows the same spring with both ends free and attached to a mass m at either end. Each end of the spring in Fig. 14.26(b) is stretched by the same force F.

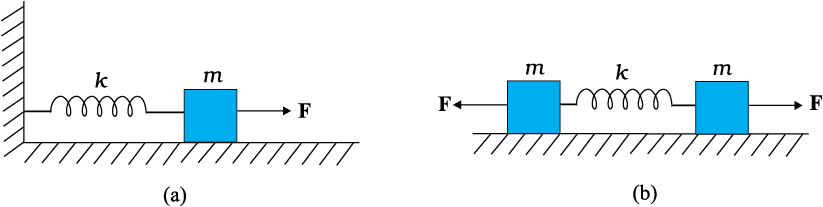
Fig. 14.26

(a) What is the maximum extension of the spring in the two cases?

(b) If the mass in Fig. (a) and the two masses in Fig. (b) are released, what is the period of oscillation in each case?

NEET SOLUTION:

For one block system:
Let the extension l is produced when a force F is applied to the free end of the spring. For the maximum extension,
F = kl
Where k is the spring constant.
Hence, the maximum extension, $l = \frac{F}{k}$
For the two-block system:
The displacement (x) produced is:
$x = \frac{l}{2}$
$Net force, F = + 2 kx = 2 k \frac{l}{2}$
$∴ l = \frac{F}{k}$
$For one block system :$
$For mass (m) of the block,$
$F = ma = m \frac{d^{2} x}{{dt}^{2}}$
$where x is the displacement of the block in time t .$
$∴ m \frac{d^{2} x}{{dt}^{2}} = - kx$
$Negative sign shows that the direction of elastic force is opposite to the direction of displacement .$
$\frac{d^{2} x}{{dt}^{2}} = - (\frac{k}{m}) x = - ω^{2} x$
$where ω^{2} = \frac{k}{m}$
$ω = \sqrt{\frac{k}{m}}$
$∴ Time period of the oscillation, T = \frac{2 π}{ω} = \frac{2 π}{\sqrt{\frac{k}{m}}} = 2 π \sqrt{\frac{m}{k}}$
$For the two block system :$
$F = m \frac{d^{2} x}{{dt}^{2}}$
$m \frac{d^{2} x}{{dt}^{2}} = - 2 kx$
$\frac{d^{2} x}{{dt}^{2}} = - [\frac{2 k}{m}] x = - ω^{2} x$
$where,$
$Angular frequency, ω = \sqrt{\frac{2 k}{m}}$
$∴ Time period, T = \frac{2 π}{ω} = 2 π \sqrt{\frac{m}{2 k}}$

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions