You may find the following data useful in solving the exercises:
e = 1.6×10–19C
N = 6.023×1023 per mole
1/(4πε0) = 9 × 109 N m2/C2
k = 1.381×10–23J 0K–1
1 MeV = 1.6×10–13 J
1 u = 931.5 MeV/c2
1 year = 3.154×107 s
mH = 1.007825 u
mn = 1.008665 u
m(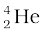 ) = 4.002603 u
) = 4.002603 u
me = 0.000548 u
13.1 (a) Two stable isotopes of lithium 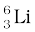 and
and 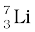 have respective abundances of 7.5% and 92.5%. These isotopes have masses 6.01512 u and 7.01600 u, respectively. Find the atomic mass of lithium.
have respective abundances of 7.5% and 92.5%. These isotopes have masses 6.01512 u and 7.01600 u, respectively. Find the atomic mass of lithium.
(b) Boron has two stable isotopes, 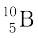 and
and 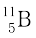 . Their respective masses are 10.01294 u and 11.00931 u, and the atomic mass of boron is 10.811 u. Find the abundances of
. Their respective masses are 10.01294 u and 11.00931 u, and the atomic mass of boron is 10.811 u. Find the abundances of 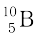 and
and 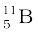 .
.

© 2026 GoodEd Technologies Pvt. Ltd.