Ncert Exercises & Solutions

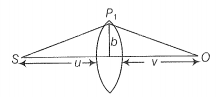
(i) Consider a thin lens placed between a source (S) and an observer (O) (Figure). Let the thickness of the lens vary as $w (b) = w_{0} - \frac{b^{2}}{α}$ , where b is the verticle distance from the pole, $w_{0}$ is a constant. Using Fermat's principle i.e., the time of transit for a ray between the source and observer is an extremum, find the condition that all paraxial rays starting from the source will converge at a point O on the axis. Find the focal length.

(ii) A gravitational lens may be assumed to have a varying width of the form
                   $w (b) = k_{1} \ln (\frac{k_{2}}{b}) b_{\min} < b < b_{\max}$
                             $= k_{1} \ln (\frac{k_{2}}{b_{\min}}) b < b_{\min}$
Show that an observer will see an image of a point object as a ring about the centre of the lens with an angular radius
                             $β = \sqrt{\frac{(n - 1) k_{1} \frac{u}{v}}{u + v}}$

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions