If light passes near a massive object, the gravitational interaction causes of bending of the ray. This can be thought of as happening due to a change in the effective refractive index of the medium given by,
n(r)=1+2 GM/rc2
where r is the distance of the point of consideration from the centre of the mass of the massive body, G is the universal gravitational constant, M the mass of the body and c the speed of light in the vacuum. Considering a spherical object find the deviation of the ray from the original path as it grazes the object.
Hint: The deviation of light depends on the refractive index of the object.
Step 1: Use Snell's law.
Let us consider two planes at r and r+dr. Let the light be incident at an angle at the plane at r and leave r + dr at an angle +d. Then from Snell's law,
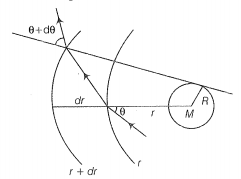
n(r)sin= n(r + dr) sin( + d)
n(r) sin =
As
n(r) sin=
Ignoring the product of differentials;
Or we have,
Step 2: Integrate both sides.
Now, substitution for integrals, we have,
Now,
2rdr= 2xdx
Put
This is the required proof.

© 2026 GoodEd Technologies Pvt. Ltd.