Hint: The image distance in the first case will the object distance in the second or vice-versa.

Step 1: Find the object distance and the image distance.

The principle of reversibility states that the position of object and image are interchangeable.
So, by the reversibility of u and v, as seen from the formula for the lens,
                                          $\frac{1}{\mathrm{f}}=\frac{1}{\mathrm{v}}-\frac{1}{\mathrm{u}}$
it is clear that there are two positions for which there shall be an image.
Let the first position be on the stream when the lens is at O. Finding u and v and substituting in lens formula.
Given,                         -u+v=D
$\Rightarrow$                              u = -(D-v)
Placing it in the lens formula,
                                   $\frac{1}{\mathrm{v}}-\frac{1}{-\left(\mathrm{D}-\mathrm{v}\right)}=\frac{1}{\mathrm{f}}$

On solving, we have,
$\Rightarrow$                             $\frac{\mathrm{v}+\mathrm{D}-\mathrm{v}}{(\mathrm{D}-\mathrm{v})\mathrm{v}}=\frac{1}{\mathrm{f}}$

$\Rightarrow$                             ${\mathrm{v}}^2-\mathrm{Dv}+\mathrm{Df}=0$
$\Rightarrow$                             $\mathrm{v}=\frac{\mathrm{D}}{2}\pm \frac{\sqrt{{\mathrm{D}}^2-4\mathrm{Df}}}{2}$
Hence,
                     $\mathrm{u}=-(\mathrm{D}-\mathrm{v})=-\left(\frac{\mathrm{D}}{2}\pm \frac{\sqrt{{\mathrm{D}}^2-4\mathrm{Df}}}{2}\right)$

              
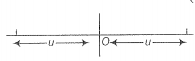
When the object distance = $\frac{\mathrm{D}}{2}+\frac{\sqrt{{\mathrm{D}}^2-4\mathrm{Df}}}{2}$
The image distance = $\frac{\mathrm{D}}{2}-\frac{\sqrt{{\mathrm{D}}^2-4\mathrm{Df}}}{2}$
Similarly, when the object distance = $\frac{\mathrm{D}}{2}-\frac{\sqrt{{\mathrm{D}}^2-4\mathrm{Df}}}{2}$
The image distance = $\frac{\mathrm{D}}{2}+\frac{\sqrt{{\mathrm{D}}^2-4\mathrm{Df}}}{2}$
The distance between the points for these two object distance =$\frac{\mathrm{D}}{2}+\frac{\sqrt{{\mathrm{D}}^2-4\mathrm{Df}}}{2}-\left(\frac{\mathrm{D}}{2}-\frac{\sqrt{{\mathrm{D}}^2-4\mathrm{Df}}}{2}\right)=\sqrt{{\mathrm{D}}^2-4\mathrm{Df}}$

Step 2: Find the magnification in the two cases.
Let                                        $\mathrm{d}=\sqrt{{\mathrm{D}}^2-4\mathrm{Df}}$
If $\mathrm{u}=\frac{\mathrm{D}}{2}+\frac{\mathrm{d}}{2}$, then the image is at v = $\frac{\mathrm{D}}{2}-\frac{\mathrm{d}}{2}$
$\therefore$ The magnification, ${\mathrm{m}}_1=\frac{\mathrm{D}-\mathrm{d}}{\mathrm{D}+\mathrm{d}}$
If $\mathrm{u}=\frac{\mathrm{D}-\mathrm{d}}{2}$, then v=$\frac{\mathrm{D}+\mathrm{d}}{2}$
$\therefore$ The magnification, ${\mathrm{m}}_2=\frac{\mathrm{D}+\mathrm{d}}{\mathrm{D}-\mathrm{d}}$
Thus, $\frac{{\mathrm{m}}_2}{{\mathrm{m}}_1}={\left(\frac{\mathrm{D}+\mathrm{d}}{\mathrm{D}-\mathrm{d}}\right)}^2$
This is the required expression of magnification.