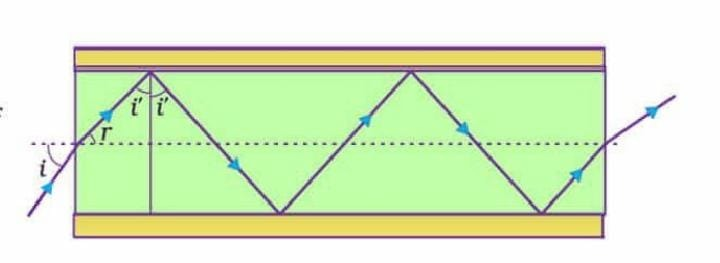
(a)
Hint: Total internal reflection occurs when the ray goes from a danser medium to a rarer medium.
Step 1: Find the angle of refraction at the inner core and outer core interface.
Refractive index of the glass fibre, ${\mu }_1$ = 1.68
Refractive index of the outer covering of the pipe, ${\mu }_2$= 1.44
For total internal reflection,
The angle of refraction at the inner core and outer core interface: $\mathrm{r}=90°$
The angle of incidence at the interface =i'
Refractive index of the inner core with respect to the outer core:

$\mu =\frac{{\mu }_1}{{\mu }_2}=\frac{1}{\sin i\text{'}}$
$\sin i\text{'}=\frac{{\mu }_2}{{\mu }_1}$
$=\frac{1.44}{1.68}=0.8571$
$\therefore i\text{'}={59}^{°}$

Step 2: Find the maximum angle of incidence.
Maximum angle of refraction at the air-glass interface,

$r_{max}=90°-i\text{'}=90°-59°=31°$

Let, $i_{max}$ be the maximum angle of incidence.

The refractive index of glass fibre w.r.t. air,

${\mu }_1=\frac{\sin i_{max}}{\sin r_{max}}$
$$
$\sin i_{max}={\mu }_1\sin r_{max}$
$=1.68\sin 31°$
$= 1.68\times 0.510$
$=0.8652$
$\therefore i_{max}={\sin }^{-1}0.8652\approx 60°$
Thus, all the rays incident at angles lying in the range 0 <i< 60° will suffer total internal reflection.

(b)
Hint: Total internal reflectionm occurs when the ray goes from a danser medium to a rarer medium.
Step 1: Find the angle of refraction at the inner core and outer core interface.
If there is no outer covering of the pipe,
The angle of refraction at the air - pipe interface, r= 90°,
According to Snell's law,

$\frac{\sin r}{\sin i}={\mu }_1=1.68$
$\sin \mathrm{i\text{'}}=\frac{\sin 90°}{1.68}=\frac{1}{1.68}$
$\mathrm{i\text{'}}={\sin }^{-1}(0.5952)$
$=36.5°$

Step 2: Find the maximum angle of incidence.
For maximum angle of inncidence, \(i=90^o\),
\(r_{max}=36.5^o\) and \(i'=53.5^o\)
which greater than critical angle.
Thus, all the rays incident at angles lying in the range \(53.5^o\) <i< 90° will suffer total internal reflection.