Ncert Exercises & Solutions

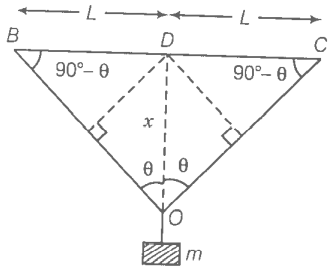
A mild steel wire of length \(2L\) and cross-sectional area \(A\) is stretched, well within the elastic limit, horizontally between two pillars (figure). A mass \(m\) is suspended from the mid-point of the wire. Strain in the wire is:

1.	\( \dfrac{x^2}{2 L^2} \)	2.	\(\dfrac{x}{\mathrm{~L}} \)
3.	\(\dfrac{x^2}{L}\)	4.	\(\dfrac{x^2}{2L}\)

(1) Hint: Use Pythagoras theorem to find the change in length.

Step 1: Find the change in length.

Consider the diagram below

Hence, change in length

∆ L = BO + OC - (BD + DC)

= 2 BO - 2 BD (∴ BO = OC, BD = DC)

= 2 [BO - BD]

= 2 [{(x^{2} + L^{2})}^{\frac{1}{2}} - L]

= 2 L [{(1 + \frac{x^{2}}{L^{2}})}^{\frac{1}{2}} - 1]

= 2 L [(1 + \frac{x^{2}}{2 L^{2}}) - 1] = \frac{x^{2}}{L}

Step 2: Find the strain.

Strain = \frac{∆ L}{L} = \frac{x^{2}}{2 L^{2}}

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions