Ncert Exercises & Solutions

Question 7. 18. A solid sphere rolls down two different inclined planes of the same heights but different angles of inclination, (a) Will it reach the bottom with the same speed in each case? (b) Will it take longer to roll down one plane than the other? (c) If so, which one and why?

(a)Mass of the sphere = m

Height of the plane = h

The velocity of the sphere at the bottom of the plane = v

At the top of the plane, the total energy of the sphere = Potential energy = mgh

At the bottom of the plane, the sphere has both translational and rotational kinetic energies.

Hence, total energy =

\frac{1}{2} {mv}^{2} + \frac{1}{2} {Iω}^{2}

Using the law of conservation of energy,

\frac{1}{2} {mv}^{2} + \frac{1}{2} {Iω}^{2} = mgh

...(i)

For a solid sphere, the moment of inertia about its center,

I = \frac{2}{5} {mr}^{2}

Hence, equation (i) becomes:

\begin{array}{l} \frac{1}{2} {mv}^{2} + \frac{1}{2} (\frac{2}{5} {mr}^{2}) ω^{2} = mgh \\ \frac{1}{2} v^{2} + \frac{1}{5} r^{2} ω^{2} = gh \end{array}

\begin{array}{l} \Rightarrow \frac{1}{2} v^{2} + \frac{1}{5} v^{2} = g h (a s v = r ω) \\ v^{2} (\frac{7}{10}) = g h \\ v = \sqrt{\frac{10}{7} g h} \end{array}

Therefore, the velocity at the bottom remains the same from whichever inclined plane the sphere is rolled.

(b),(c)

Consider two inclined planes with inclinations

θ_{1}

and

θ_{2}

, related as:

θ_{1}

θ_{2}

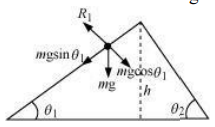
The acceleration produced in the sphere when it rolls down the plane inclined at

θ_{1}

is,

a_{1} =

g sin

θ_{1}

The various forces acting on the sphere are shown in the following figure.

R_{1}

is the normal reaction to the sphere.
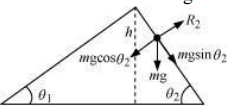
Similarly, the acceleration produced in the sphere when it rolls down the plane inclined at

θ_{2}

is,

a_{2}

= g sin

θ_{2}

The various forces acting on the sphere are shown in the following figure.

R_{2}

is the normal reaction to the sphere.

\begin{array}{l} θ_{2} > θ_{1} \\ \sin θ_{2} > \sin θ_{1} \dots (i) \\ \Rightarrow a_{2} > a_{1} \dots (ii) \end{array}

Initial velocity, u = 0
Final velocity, v = Constant
Using the first equation of motion, we can obtain the time of roll as:
v = u + at

\Rightarrow t \propto \frac{1}{a}

[For inclination θ_{1}, t_{1} \propto \frac{1}{a_{1}}]

For inclination θ_{2}, t_{2} \propto \frac{1}{a_{2}} . . . (iii)

From equations (ii) and (iii), we get:

t_{2} < t_{1}

Hence, the sphere will take a longer time to reach the bottom of the inclined plane having a smaller inclination.

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions