Q. 33 A bob of mass m suspended by a light string of length L is whirled into a vertical circle as shown in the figure.
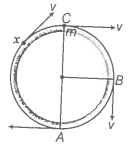
What will be the trajectory of the particle, if the string is cut at
(a) point B?
(b) point C?
(c) point X?
When the bob is whirled into a vertical circle, the required centripetal force is obtained from the tension in the string. When the string is cut, the tension in the string becomes zero, and force is not provided, hence, starts to move in a straight line path along the direction of its velocity.
(a) At point B. the velocity of B is vertically downward. therefore, when the string is cut at B, bob moves vertically downward.
(b) At point C, the velocity is along the horizontal towards the right, therefore, when the string is cut at C, bob moves horizontally towards the right.
Also, the bob moves under gravity simultaneously with horizontal uniform speed. So, traversed on a parabolic path with vertex at C.
(c) At point X, the velocity of the bob is along the tangent drawn at point X, therefore when string is cut at C. bob moves along the tangent at that point X. Also, the bob moves under gravity simultaneously with horizontal uniform speed. So, traversed on a parabolic path with vertex higher than C.


© 2026 GoodEd Technologies Pvt. Ltd.