Ncert Exercises & Solutions

Question 6.4:

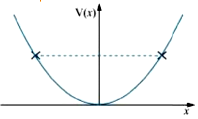
The potential energy function for a particle executing linear simple harmonic motion is given by V(x) = $k x^{2} / 2$ , where k is the force constant of the oscillator. For k = 0.5 N/m, the graph of V(x) versus x is shown in Fig. 6.12. Show that a particle of total energy 1 J moving under this potential must ‘turn back’ when it reaches x = ± 2 m.

$G i v e n,$
$k = 0.5 N m^{- 1}$
$T o t a l e n e r g y, E = 1 J$
$T h e p a r t i c l e c a n g o u p t o a m a x i m u m d i s \tan c e x_{m}, w h e r e i t s t o t a l e n e r g y$
$c h a n g e d i n t o e l e s t i c p o t e n t i a l e n e r g y .$
$H e n c e,$
$\frac{1}{2} k {x_{m}}^{2} = E$
$\Rightarrow x_{m} = \sqrt{\frac{2 E}{k}} = \sqrt{\frac{2 \times 1}{0.5}}$
$\Rightarrow x_{m} = \pm 2$

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions