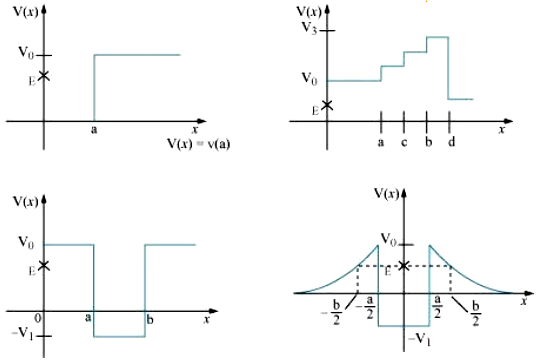
We know that total energy, E = K.E. + P.E.

Or, K.E. = E – P.E.

 Kinetic energy can not be negative. The object can not exist in the region, where its K.E. would become negative.
(a) In the region between x = 0 and x = a, potential energy is zero. So, kinetic energy is positive. In the region x,> a the potential energy has a value greater than E. So, kinetic energy will be negative in this region. Thus the particle cannot be present in the region x > a.

The minimum total energy that the particle can have in this case is zero.

(b) Here P.E. > E, the total energy of the object and as such the kinetic energy of the object would be negative. Thus objects cannot be present in any region of the graph.

(c) Here x = 0 to x = a and x > b, the P.E. is more than E, so K.E. is negative. The particle can not exist in these portions.

(d) The object can not exist in the region between x = -b/2 to x =-a/2 and x = -a/2 to x = -b/2 .Because in this region P.E. > E.