A batsman deflects a ball by an angle of 45° without changing its initial speed which is equal to 54 km/h. What is the impulse imparted to the ball? (Mass of the ball is 0.15 kg.)
The given situation can be represented as shown in the following figure.
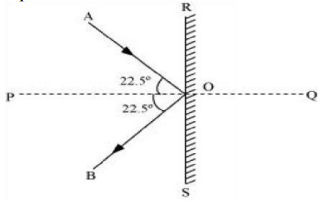
Where,
AO = Incident path of the ball
OB = Path followed by the ball after a deflection
∠AOB = Angle between the incident and deflected paths of the ball = 45°
∠AOP = ∠BOP = 22.5° = θ
Initial and final velocities of the ball = v
Horizontal component of the initial velocity = vcos θ along RO
Vertical component of the initial velocity = vsin θ along PO
Horizontal component of the final velocity = vcos θ along OS
Vertical component of the final velocity = vsin θ along OP
The horizontal components of velocities suffer no change. The vertical components of velocities are in the opposite directions.
∴Impulse imparted to the ball = Change in the linear momentum of the ball
Mass of the ball, m = 0.15 kg
Velocity of the ball, v = 54 km/h = 15 m/s
Thus,
Impulse = 2 × 0.15 × 15 cos 22.5° = 4.16 kg m/s

© 2026 GoodEd Technologies Pvt. Ltd.